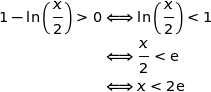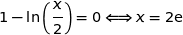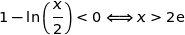Sujet et corrigé de l'exercice 4 du bac S de maths d'avril 2016 à Pondichéry
Cacher les corrigés
Soit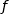 
la fonction définie sur 
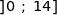par
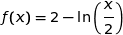
La courbe représentative 
de la fonction est donnée dans le repère orthogonal d'origine O ci-dessous :
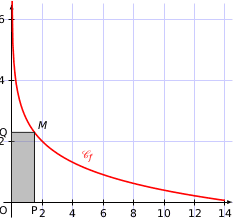
A tout point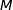 
appartenant à on associe le point 
projeté orthogonal de 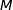sur l'axe des abscisses, et le point 
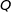projeté orthogonal de 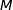sur l'axe des ordonnées.
L'aire du rectangle
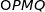est-elle constante quelle que soit la position du
point 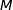sur ?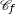
L'aire du rectangle
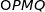peut-elle être maximale ?Si oui, préciser les coordonnées du point
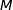correspondant.
Justifier les réponses.
Soit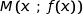 
appartenant à , alors 
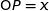et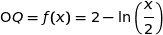 
.
Du coup l'aire de 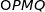est 
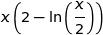u.a.
Cette expression n'est pas constante donc l'aire du rectangle n'est pas constante.
On étudie maintenant la fonction définie su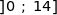r 
par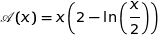 
.
Cette fonction est dérivable sur l'intervalle considéré et on a :
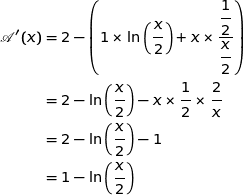
On étudie sur 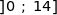le signe de 
:
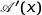On a le tableau de variations :
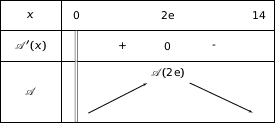
Donc la fonction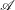 
admet un maximum sur 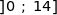atteint pour 
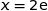. Le point M a pour ordonnée :
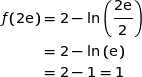
Donc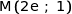 
.
