Sujet et corrigé de l'exercice 5 du bac S de maths de mai 2016 au Liban
Cacher les corrigés
On considère la suite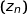 
de nombres complexes définie pour tout entier naturel 
par :
Dans le plan rapporté à un repère orthonormé, on note 
le point d'affixe 
.
On considère le nombre complexe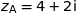 
et A le point du plan d'affixe 
.
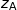1. Soit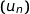 
la suite définie pour tout entier naturel par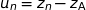 
.
a) Montrer que, pour tout entier naturel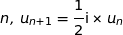 
.
Pour tout entier naturel :
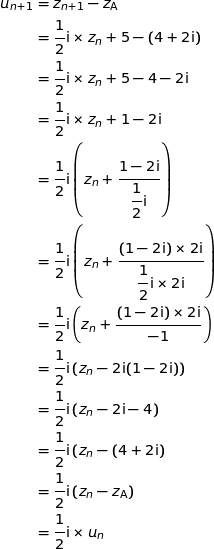
b) Démontrer que, pour tout entier naturel :
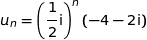
Soit 
: « 
»
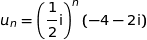Montrons par récurrence que 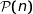est vraie pour tout entier naturel .
Initialisation au rang 0
D'un part :
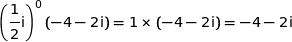
D'autre part :
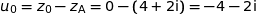
Donc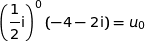 
et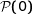 
est vraie.
Hérédité
Supposons qu'à un rang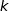 
, 
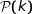soit vraie : 
.
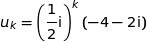Montrons qu'alors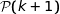 
est vraie.
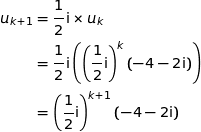
Donc 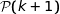est vraie.
Ainsi 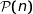est vraie pour 
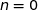et est héréditaire donc 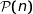est vraie pour tout entier naturel .
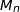2. Démontrer que, pour tout entier naturel , les points A, et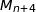 
sont alignés.
Pour prouver l'alignement des points considérés on compare pour tout entier naturel :
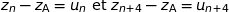
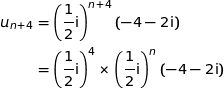
avec :
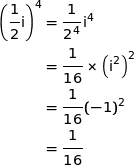
Du coup :
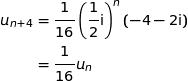
et pour tout entier naturel :
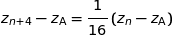
cela montre que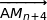 
et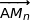 
sont colinéaires et donc que les points A, 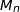et 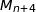sont alignés.
