Corrigé de l'exercice 3 du bac S de maths 2011 au Liban
Cacher les corrigés
Partie A : Restitution organisée de connaissances
Prérequis : On suppose connu le résultat suivant : Quels que soient les nombres complexes non nuls et
et 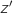 :
:
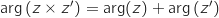 à
à 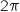 près.
Démontrer que, quels que soient les nombres complexes non nuls
près.
Démontrer que, quels que soient les nombres complexes non nuls  et
et 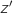 , on a :
, on a :
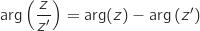 à
à  près.
près.
Il faut commencer par montrer que pour  ,
, 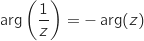 :
On peut alors montrer la relation :
:
On peut alors montrer la relation : 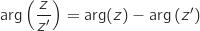 :
:
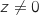 ,
, 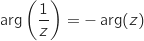 :
On peut alors montrer la relation :
:
On peut alors montrer la relation : 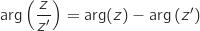 :
:
Partie B
Dans le plan complexe muni d'un repère orthonormal direct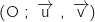 , on considère les points A et B d'affixes respectives :
, on considère les points A et B d'affixes respectives :
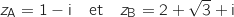
 .
.
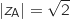
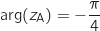
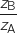 sous forme algébrique.
sous forme algébrique.
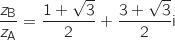
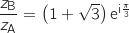 .
.
On écrit 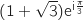 sous forme algébrique, ce qui donne :
sous forme algébrique, ce qui donne :
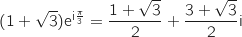 , soit l'expression qu'on a trouvé dans la question 2.a.
, soit l'expression qu'on a trouvé dans la question 2.a.
c. En déduire la forme exponentielle de 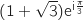 sous forme algébrique, ce qui donne :
sous forme algébrique, ce qui donne :
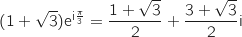 , soit l'expression qu'on a trouvé dans la question 2.a.
, soit l'expression qu'on a trouvé dans la question 2.a.
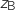 .
.
Avec le module et l'argument de 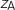 trouvé dans la question 1., on peut écrire
trouvé dans la question 1., on peut écrire 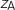 sous forme
exponentielle ce qui donne :
sous forme
exponentielle ce qui donne :
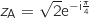 et comme
et comme
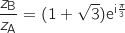 , on obtient :
, on obtient :
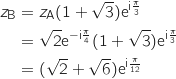
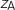 trouvé dans la question 1., on peut écrire
trouvé dans la question 1., on peut écrire 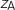 sous forme
exponentielle ce qui donne :
sous forme
exponentielle ce qui donne :
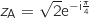 et comme
et comme
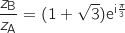 , on obtient :
, on obtient :
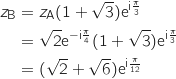
La fin de l'exercice initial faisait intervenir les transformations du plan en écriture complexe. Cette notion
ne figure plus dans les programmes depuis la rentrée 2012.
