Corrigé de l'exercice 3 du bac S de maths 2011 dans les centres étrangers
Cacher les corrigés
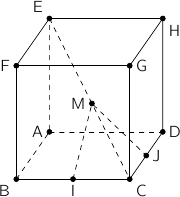
La figure ci-dessous représente un cube ABCDEFGH d'arête 1. On désigne par I et J les milieux respectifs des arêtes [BC] et [CD]. Soit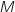 un point quelconque du segment [CE].
Dans tout l'exercice, on se place dans le repère orthonormal
un point quelconque du segment [CE].
Dans tout l'exercice, on se place dans le repère orthonormal 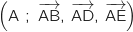 .
.
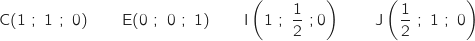 .
.
b. Justifier l'existence d'un réel
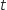 appartenant à l'intervalle
appartenant à l'intervalle 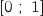 , tel que les coordonnées du point M soient
, tel que les coordonnées du point M soient 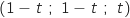 .
.
On a 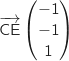 .
Les points M sont tels que
.
Les points M sont tels que 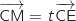 avec
avec 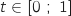 .
On a donc :
.
On a donc : 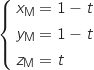
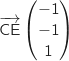 .
Les points M sont tels que
.
Les points M sont tels que 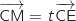 avec
avec 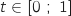 .
On a donc :
.
On a donc : 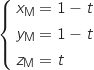
2.a. Démontrer que les points C et E appartiennent au plan médiateur du segment [IJ].
Compte tenu de la position de I et J, on a 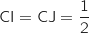 , donc C est dans le plan médiateur de [IJ].
Pour E en calculant les distances on a :
, donc C est dans le plan médiateur de [IJ].
Pour E en calculant les distances on a : 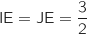 , donc E est également dans le
plan médiateur de [IJ].
, donc E est également dans le
plan médiateur de [IJ].
b. En déduire que le triangle MIJ est un triangle isocèle en M.
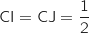 , donc C est dans le plan médiateur de [IJ].
Pour E en calculant les distances on a :
, donc C est dans le plan médiateur de [IJ].
Pour E en calculant les distances on a : 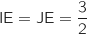 , donc E est également dans le
plan médiateur de [IJ].
, donc E est également dans le
plan médiateur de [IJ].
D'après la question précédente la droite (EC) est dans le plan médiateur de [IJ], donc tout point de cette droite aussi,
et en particulier M est équidistant de I et J, soit 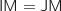 , donc MIJ est isocèle en M.
, donc MIJ est isocèle en M.
c. Exprimer 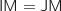 , donc MIJ est isocèle en M.
, donc MIJ est isocèle en M.
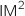 en fonction de
en fonction de 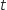 .
.
En utilisant la formule de la distance on a : 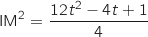 .
.
3. Le but de cette question est de déterminer la position du point M sur le segment [CE] pour laquelle la mesure de l'angle 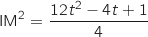 .
.
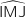 est maximale.
On désigne par
est maximale.
On désigne par 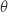 la mesure en radian de l'angle
la mesure en radian de l'angle 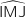 .
a. En admettant que la mesure
.
a. En admettant que la mesure 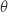 appartient à l'intervalle
appartient à l'intervalle 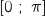 , démontrer que la mesure
, démontrer que la mesure 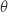 est maximale lorsque
est maximale lorsque 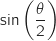 est maximal.
est maximal.
Si 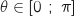 , alors
, alors 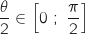 .
On a les équivalences :
.
On a les équivalences : 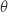 maximal
maximal  maximal
maximal 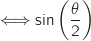 maximal (car sur
maximal (car sur 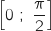 , la fonction sinus est croissante).
, la fonction sinus est croissante).
b. En déduire que la mesure est maximale lorsque la longueur IM est minimale.
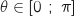 , alors
, alors 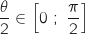 .
On a les équivalences :
.
On a les équivalences : 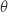 maximal
maximal  maximal
maximal 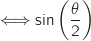 maximal (car sur
maximal (car sur 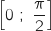 , la fonction sinus est croissante).
, la fonction sinus est croissante).
Soit K le milieu de [IJ], on travaille dans MIK rectangle en K.
Dans ce triangle : 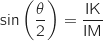 .
Dans cette expression IK est fixe, et IM est au dénominateur, donc
lorsqu'il est est minimal,
.
Dans cette expression IK est fixe, et IM est au dénominateur, donc
lorsqu'il est est minimal, 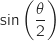 est maximal.
est maximal.
c. Etudier les variations de la fonction 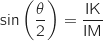 .
Dans cette expression IK est fixe, et IM est au dénominateur, donc
lorsqu'il est est minimal,
.
Dans cette expression IK est fixe, et IM est au dénominateur, donc
lorsqu'il est est minimal, 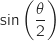 est maximal.
est maximal.
 définie sur l'intervalle
définie sur l'intervalle 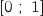 par :
par :
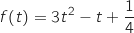
C'est une fonction trinôme du second degré on a directement son tableau de variations :
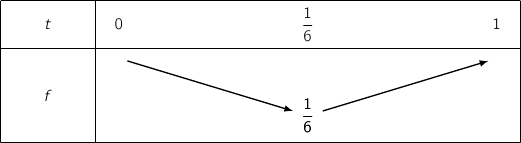
d. En déduire qu'il existe une unique position 
 du point M sur le segment [EC] telle que la mesure de l'angle
du point M sur le segment [EC] telle que la mesure de l'angle  soit maximale.
soit maximale.
On remarque que 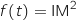 , donc d'après ce qui précède, le point
, donc d'après ce qui précède, le point 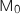 est obtenu pour
est obtenu pour 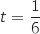 , soit
, soit 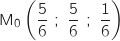 .
.
e. Démontrer que le point 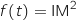 , donc d'après ce qui précède, le point
, donc d'après ce qui précède, le point 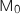 est obtenu pour
est obtenu pour 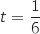 , soit
, soit 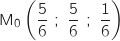 .
.
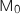 est le projeté orthogonal du point I sur le segment [EC].
est le projeté orthogonal du point I sur le segment [EC].
Le point 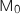 réalise la plus petite distance entre (EC) et I, donc
réalise la plus petite distance entre (EC) et I, donc 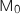 est le projeté orthogonal
de I sur (EC).
est le projeté orthogonal
de I sur (EC).
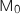 réalise la plus petite distance entre (EC) et I, donc
réalise la plus petite distance entre (EC) et I, donc 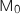 est le projeté orthogonal
de I sur (EC).
est le projeté orthogonal
de I sur (EC).
