Corrigé de l'exercice 2 du bac S de maths 2011 dans les centres étrangers
Cacher les corrigés
Les cinq questions sont indépendantes.Pour chaque question une affirmation est proposée. Indiquer si elle est vraie ou fausse, en justifiant la réponse. Une réponse qui n'est pas justifiée ne sera pas prise en compte.
Toute justification incomplète sera valorisée.
Question 1
On considère, dans le plan complexe muni d'un repère orthonormal direct , les points A, B et C d'affixes respectives :
, les points A, B et C d'affixes respectives :
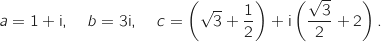
On calcule :
AB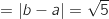 AC
AC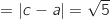 BC
BC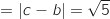 Du coup, AB
Du coup, AB AC
AC BC
BC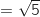 , donc l'affirmation est VRAIE.
Autre méthode :
On calcule :
, donc l'affirmation est VRAIE.
Autre méthode :
On calcule :
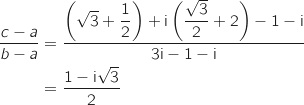 On a
On a 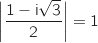 et
et 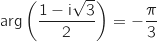 .
On en déduit que
.
On en déduit que 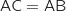 et que
et que 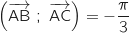 , donc que le triangle ABC est équilatéral.
L'affirmation est donc VRAIE.
, donc que le triangle ABC est équilatéral.
L'affirmation est donc VRAIE.
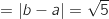 AC
AC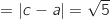 BC
BC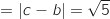 Du coup, AB
Du coup, AB AC
AC BC
BC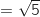 , donc l'affirmation est VRAIE.
Autre méthode :
On calcule :
, donc l'affirmation est VRAIE.
Autre méthode :
On calcule :
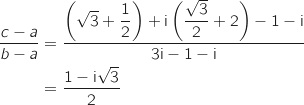 On a
On a 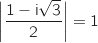 et
et 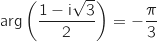 .
On en déduit que
.
On en déduit que 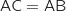 et que
et que 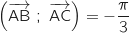 , donc que le triangle ABC est équilatéral.
L'affirmation est donc VRAIE.
, donc que le triangle ABC est équilatéral.
L'affirmation est donc VRAIE.
Question 2
Dans le sujet original cette question porte sur les transformations en écriture complexe qui ne sont plus
au programme à partir de l'année 2012-2013.
Question 3
On considère le nombre complexe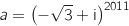 .
Affirmation
Le nombre complexe
.
Affirmation
Le nombre complexe 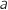 est un nombre imaginaire pur.
est un nombre imaginaire pur.
On détermine déjà un argument de 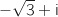 , on trouve :
, on trouve : 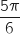 .
Donc
.
Donc 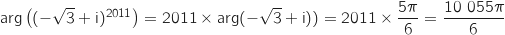 .
La mesure principale de
.
La mesure principale de 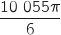 est
est 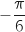 , comme elle est différente de
, comme elle est différente de 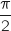 et de
et de 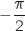 , le nombre complexe considéré n'est pas imaginaire pur.
L'affirmation est FAUSSE.
, le nombre complexe considéré n'est pas imaginaire pur.
L'affirmation est FAUSSE.
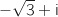 , on trouve :
, on trouve : 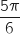 .
Donc
.
Donc 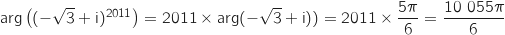 .
La mesure principale de
.
La mesure principale de 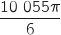 est
est 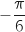 , comme elle est différente de
, comme elle est différente de 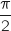 et de
et de 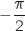 , le nombre complexe considéré n'est pas imaginaire pur.
L'affirmation est FAUSSE.
, le nombre complexe considéré n'est pas imaginaire pur.
L'affirmation est FAUSSE.
Question 4
Soit une variable aléatoire qui suit la loi exponentielle de paramètre
une variable aléatoire qui suit la loi exponentielle de paramètre 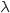 , où
, où 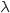 est un nombre strictement positif.
On rappelle que, pour tout réel
est un nombre strictement positif.
On rappelle que, pour tout réel 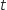 strictement positif, la probabilité de l'évènement
strictement positif, la probabilité de l'évènement 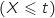 s'exprime par
s'exprime par 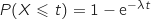 .
Affirmation
Sachant que
.
Affirmation
Sachant que 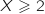 , la probabilité que
, la probabilité que  appartienne à l'intervalle
appartienne à l'intervalle 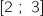 est égale à
est égale à 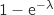 .
.
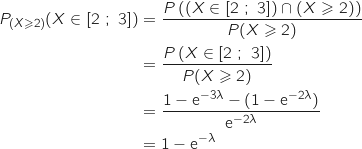 L'affirmation est VRAIE.
L'affirmation est VRAIE.
Question 5
Une urne contient au total boules dont cinq sont blanches et les autres noires.
On effectue 10 tirages successifs indépendants en remettant la boule dans l'urne après chaque tirage.
Affirmation
La plus petite valeur de l'entier
boules dont cinq sont blanches et les autres noires.
On effectue 10 tirages successifs indépendants en remettant la boule dans l'urne après chaque tirage.
Affirmation
La plus petite valeur de l'entier  , pour laquelle la probabilité d'obtenir au moins une boule noire sur les 10 tirages est supérieure ou égale à
, pour laquelle la probabilité d'obtenir au moins une boule noire sur les 10 tirages est supérieure ou égale à 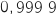 , est égale à 13.
, est égale à 13.
La variable aléatoire qui compte le nombre de boules noires obtenues en 10 tirages suit une loi
binomiale de paramètres 10 et 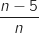 .
La probabilité d'obtenir au moins une boule noire est :
.
La probabilité d'obtenir au moins une boule noire est : 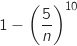 .
On résout :
.
On résout : 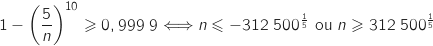 Avec
Avec 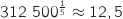 .
Donc le plus petit entier (positif)
.
Donc le plus petit entier (positif)  cherché est bien 13.
L'affirmation est VRAIE.
cherché est bien 13.
L'affirmation est VRAIE.
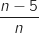 .
La probabilité d'obtenir au moins une boule noire est :
.
La probabilité d'obtenir au moins une boule noire est : 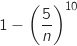 .
On résout :
.
On résout : 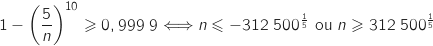 Avec
Avec 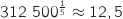 .
Donc le plus petit entier (positif)
.
Donc le plus petit entier (positif)  cherché est bien 13.
L'affirmation est VRAIE.
cherché est bien 13.
L'affirmation est VRAIE.
