Corrigé de l'exercice 4 du bac S de maths 2011 en Amérique du Nord
Cacher les corrigés
Partie A
On considère la fonction définie sur
définie sur 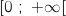 par
par
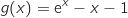
 .
.
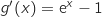 , on facilement le tableau de variations sur
, on facilement le tableau de variations sur 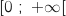 :
:
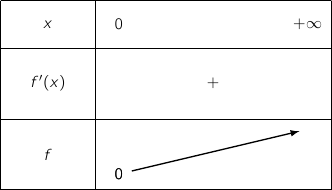
2. Déterminer le signe de
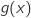 suivant les valeurs de
suivant les valeurs de  .
.
D'après le tableau de variations, on a 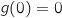 et pour
et pour 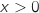 ,
, 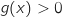 .
.
3. En déduire que pour tout 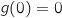 et pour
et pour 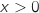 ,
, 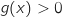 .
.
 de
de 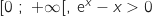 .
.
De 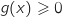 pour
pour 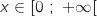 , on déduit
, on déduit 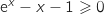 soit
soit 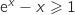 et donc
et donc 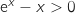 .
.
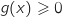 pour
pour 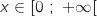 , on déduit
, on déduit 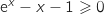 soit
soit 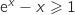 et donc
et donc 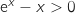 .
.
Partie B
On considère la fonction définie sur
définie sur 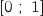 par
par
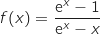
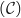 représentative de la fonction
représentative de la fonction  dans le plan muni d'un repère orthonormal est donnée ci-dessous :
dans le plan muni d'un repère orthonormal est donnée ci-dessous :
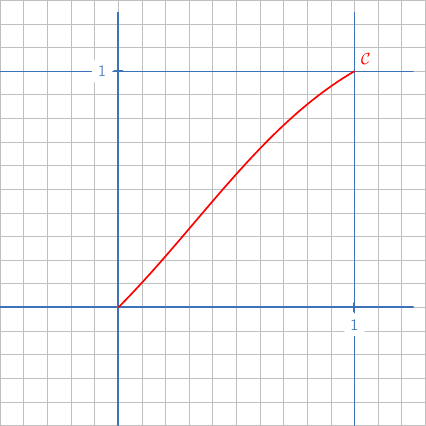
 est strictement croissante sur [0 ; 1].
est strictement croissante sur [0 ; 1].
1. Montrer que pour tout
 de [0 ; 1],
de [0 ; 1], 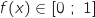 .
.
Comme  est strictement croissante sur
est strictement croissante sur 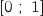 , on a le tableau de variations :
, on a le tableau de variations :
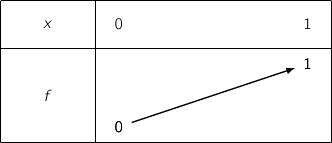
Donc pour 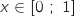 , on a bien
, on a bien 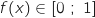 .
.
2. Soit (D) la droite d'équation  est strictement croissante sur
est strictement croissante sur 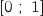 , on a le tableau de variations :
, on a le tableau de variations :

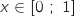 , on a bien
, on a bien 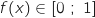 .
.
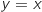 .
a. Montrer que pour tout
.
a. Montrer que pour tout  de [0 ; 1],
de [0 ; 1], 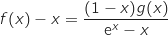 .
.
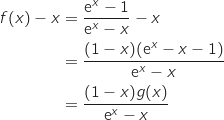
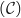 sur
sur 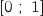 .
.
On sait que 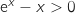 , sur
, sur 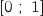 , le signe de
, le signe de 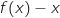 est donc le même que celui
de
est donc le même que celui
de 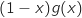 .
Sur cet intervalle
.
Sur cet intervalle 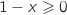 et
et 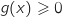 , donc
, donc 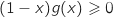 , donc
, donc 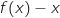 aussi et donc
aussi et donc 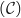 est au dessus de
est au dessus de 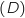 . On peut remarquer que
. On peut remarquer que 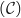 et
et 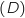 se coupent pour
se coupent pour 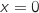 et pour
et pour 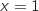 .
.
3.a. Déterminer une primitive de 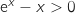 , sur
, sur 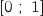 , le signe de
, le signe de 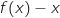 est donc le même que celui
de
est donc le même que celui
de 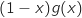 .
Sur cet intervalle
.
Sur cet intervalle 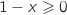 et
et 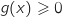 , donc
, donc 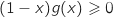 , donc
, donc 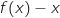 aussi et donc
aussi et donc 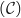 est au dessus de
est au dessus de 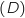 . On peut remarquer que
. On peut remarquer que 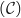 et
et 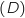 se coupent pour
se coupent pour 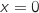 et pour
et pour 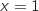 .
.
 sur
sur 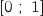 .
.
On a une fonction de la forme 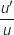 avec
avec  sur
sur 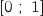 .
Donc une primitive est
.
Donc une primitive est 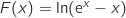 .
.
b. Calculer l'aire, en unités d'aire, du domaine du plan délimité par la courbe 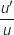 avec
avec  sur
sur 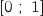 .
Donc une primitive est
.
Donc une primitive est 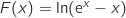 .
.
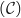 , la droite (D) et les droites d'équations
, la droite (D) et les droites d'équations 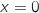 et
et 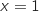 .
.
Compte tenu des positions de 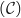 et
et 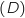 l'aire considérée est :
l'aire considérée est :
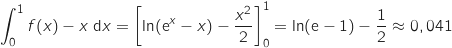 u.a.
u.a.
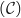 et
et 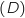 l'aire considérée est :
l'aire considérée est :
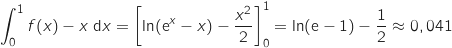 u.a.
u.a.
Partie C
On considère la suite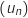 définie par :
définie par :
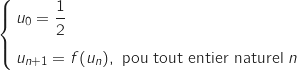
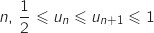 .
.
La propriété à montrer pour tout entier 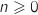 est :
est :
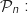 «
«
 ».
Initialisation
».
Initialisation
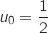 et
et 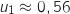 , ainsi
, ainsi 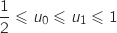 Donc
Donc 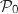 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 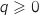 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
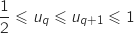 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 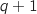 .
.
 est croissante sur
est croissante sur 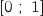 , on l'applique à l'hypothèse de récurrence :
, on l'applique à l'hypothèse de récurrence :
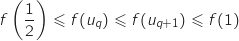 avec
avec 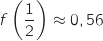 , donc
, donc 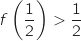 et
et 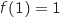 .
Il vient donc :
.
Il vient donc : 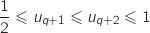 Donc
Donc 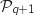 est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 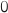 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 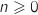 .
.
3. En déduire que la suite 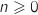 est :
est :
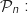 «
«
 ».
Initialisation
».
Initialisation
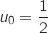 et
et 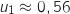 , ainsi
, ainsi 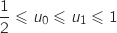 Donc
Donc 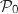 est vraie.
Hérédité
On suppose que la propriété est vraie à un rang
est vraie.
Hérédité
On suppose que la propriété est vraie à un rang 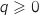 , on a donc l'hypothèse de récurrence :
, on a donc l'hypothèse de récurrence :
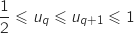 On montre qu'alors la propriété est vraie au rang
On montre qu'alors la propriété est vraie au rang 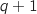 .
.
 est croissante sur
est croissante sur 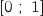 , on l'applique à l'hypothèse de récurrence :
, on l'applique à l'hypothèse de récurrence :
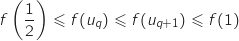 avec
avec 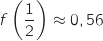 , donc
, donc 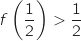 et
et 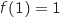 .
Il vient donc :
.
Il vient donc : 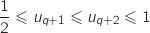 Donc
Donc 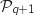 est vraie.
Ainsi la propriété est vraie au rang
est vraie.
Ainsi la propriété est vraie au rang 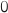 et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier
et elle est héréditaire donc selon le principe de récurrence la propriété
est vraie pour tout entier 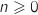 .
.
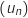 est convergente et déterminer sa limite.
est convergente et déterminer sa limite.
La suite 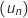 est croissante et majorée par 1, donc elle admet une limite.
La fonction
est croissante et majorée par 1, donc elle admet une limite.
La fonction  étant continue sur
étant continue sur 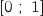 , la limite de la suite est solution de l'équation
, la limite de la suite est solution de l'équation
 .
.
Cette équation a deux solutions 0 et 1, la limite ne peut pas être 0, car la suite est croissante et son premier terme est .
On conclut que
.
On conclut que 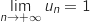 .
.
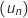 est croissante et majorée par 1, donc elle admet une limite.
La fonction
est croissante et majorée par 1, donc elle admet une limite.
La fonction  étant continue sur
étant continue sur 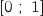 , la limite de la suite est solution de l'équation
, la limite de la suite est solution de l'équation
 .
.
Cette équation a deux solutions 0 et 1, la limite ne peut pas être 0, car la suite est croissante et son premier terme est
 .
On conclut que
.
On conclut que 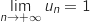 .
.
