Corrigé de l'exercice 1 du bac S de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Partie 1
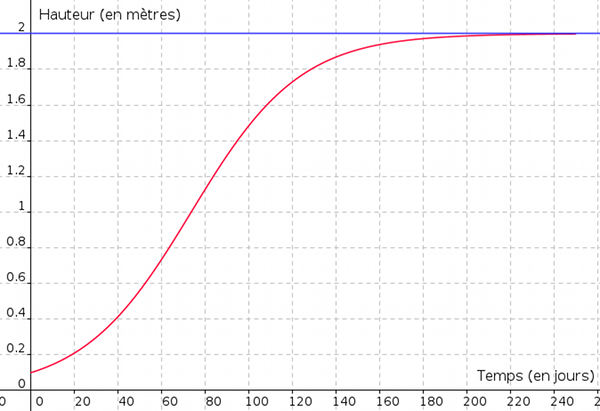
On s'intéresse à l'évolution de la hauteur d'un plant de maïs en fonction du temps. Le graphique ci-dessous représente cette évolution. La hauteur est en mètres et le temps en jours.
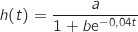
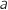 et
et 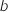 sont des constantes réelles positives,
sont des constantes réelles positives, 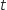 est la variable temps exprimée en jours et
est la variable temps exprimée en jours et 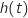 désigne
la hauteur du plant, exprimée en mètres.
On sait qu'initialement, pour
désigne
la hauteur du plant, exprimée en mètres.
On sait qu'initialement, pour 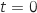 , le plant mesure 0,1 m et que sa hauteur tend vers une hauteur
limite de 2 m.
Déterminer les constantes
, le plant mesure 0,1 m et que sa hauteur tend vers une hauteur
limite de 2 m.
Déterminer les constantes 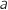 et
et 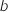 afin que la fonction
afin que la fonction 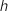 corresponde à la croissance du plant de maïs
étudié.
corresponde à la croissance du plant de maïs
étudié.
La condition 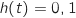 donne :
donne : 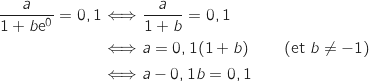 La condition
La condition 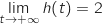 donne :
donne :
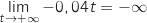 ;
par composition
;
par composition 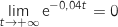 et donc
et donc
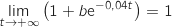 Finalement par quotient :
Finalement par quotient : 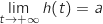 .
Du coup
.
Du coup 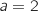 et de plus :
et de plus : 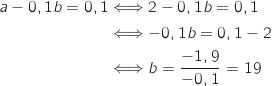 Donc
Donc 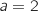 et
et 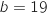 .
.
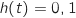 donne :
donne : 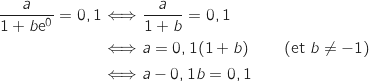 La condition
La condition 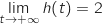 donne :
donne :
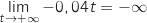 ;
par composition
;
par composition 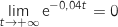 et donc
et donc
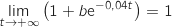 Finalement par quotient :
Finalement par quotient : 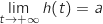 .
Du coup
.
Du coup 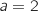 et de plus :
et de plus : 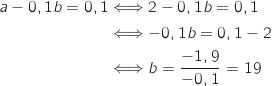 Donc
Donc 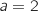 et
et 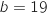 .
.
Partie 2
On considère désormais que la croissance du plant de maïs est donnée par la fonction définie sur
définie sur
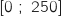 par
par
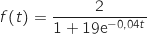
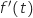 en fonction de
en fonction de 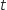 (
(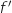 désignant la fonction dérivée de la fonction
désignant la fonction dérivée de la fonction  ).
En déduire les variations de la fonction
).
En déduire les variations de la fonction  sur l'intervalle
sur l'intervalle 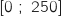 .
.
La fonction  est dérivable sur
est dérivable sur 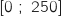 .
On utilise la formule de dérivation :
.
On utilise la formule de dérivation : 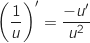 avec :
avec :
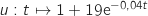 et
et 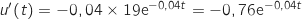 Donc
Donc 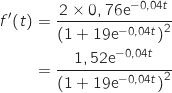 Pour tout
Pour tout 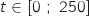 le numérateur et le dénominateur de la fraction obtenue sont strictement positifs donc la fonction
le numérateur et le dénominateur de la fraction obtenue sont strictement positifs donc la fonction  est strictement croissante sur l'intervalle considéré.
est strictement croissante sur l'intervalle considéré.
2. Calculer le temps nécessaire pour que le plant de maïs atteigne une hauteur supérieure à 1,5 m.
 est dérivable sur
est dérivable sur 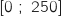 .
On utilise la formule de dérivation :
.
On utilise la formule de dérivation : 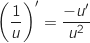 avec :
avec :
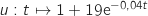 et
et 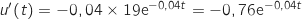 Donc
Donc 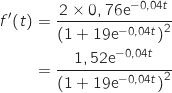 Pour tout
Pour tout 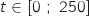 le numérateur et le dénominateur de la fraction obtenue sont strictement positifs donc la fonction
le numérateur et le dénominateur de la fraction obtenue sont strictement positifs donc la fonction  est strictement croissante sur l'intervalle considéré.
est strictement croissante sur l'intervalle considéré.
Il s'agit de résoudre l'inéquation :
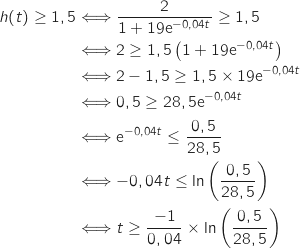 où
où 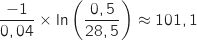 Donc le maïs dépasse la hauteur de 1,5 m à partir du 102
Donc le maïs dépasse la hauteur de 1,5 m à partir du 102 jour.
jour.
3.a. Vérifier que pour tout réel 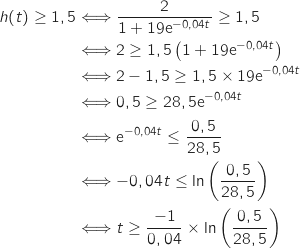 où
où 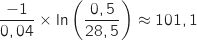 Donc le maïs dépasse la hauteur de 1,5 m à partir du 102
Donc le maïs dépasse la hauteur de 1,5 m à partir du 102 jour.
jour.
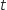 appartenant à l'intervalle
appartenant à l'intervalle 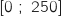 on a
on a
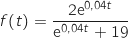
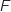 définie sur l'intervalle
définie sur l'intervalle 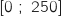 par
par 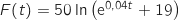 est
une primitive de la fonction
est
une primitive de la fonction  .
.
Pour tout 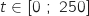 :
: 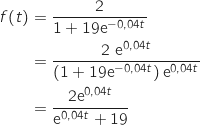 La fonction
La fonction 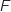 proposée est dérivable sur
proposée est dérivable sur 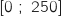 et on a en utilisant la formule de la dérivée de
et on a en utilisant la formule de la dérivée de 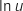 :
:
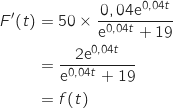 Donc
Donc 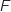 est bien une primitive de
est bien une primitive de  .
.
b. Déterminer la valeur moyenne de 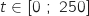 :
: 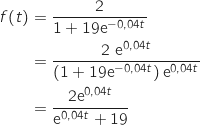 La fonction
La fonction 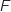 proposée est dérivable sur
proposée est dérivable sur 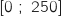 et on a en utilisant la formule de la dérivée de
et on a en utilisant la formule de la dérivée de 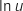 :
:
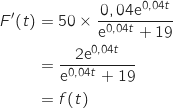 Donc
Donc 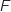 est bien une primitive de
est bien une primitive de  .
.
 sur l'intervalle
sur l'intervalle 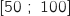 .
.
En donner une valeur approchée à
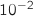 près et interpréter ce résultat.
près et interpréter ce résultat.
La valeur moyenne est définie par :
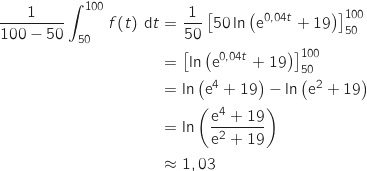 La hauteur moyenne du plant de maïs sur la période considérée (du 50
La hauteur moyenne du plant de maïs sur la période considérée (du 50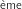 au 100
au 100 jour) est d'environ 1,03 m.
jour) est d'environ 1,03 m.
4. On s'intéresse à la vitesse de croissance du plant de maïs ; elle est donnée par la fonction dérivée
de la fonction 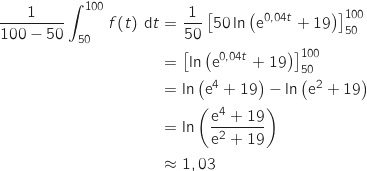 La hauteur moyenne du plant de maïs sur la période considérée (du 50
La hauteur moyenne du plant de maïs sur la période considérée (du 50 au 100
au 100 jour) est d'environ 1,03 m.
jour) est d'environ 1,03 m.
 .
La vitesse de croissance est maximale pour une valeur de
.
La vitesse de croissance est maximale pour une valeur de 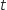 .
En utilisant le graphique, déterminer une valeur approchée de celle-ci.
Estimer alors la hauteur du plant.
.
En utilisant le graphique, déterminer une valeur approchée de celle-ci.
Estimer alors la hauteur du plant.
Le coefficient directeur de la tangente en un point de la courbe représentative de  correspond à la vitesse de croissance.
Par observation graphique ce coefficient est maximum autour de
correspond à la vitesse de croissance.
Par observation graphique ce coefficient est maximum autour de 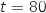 . (On peut voir cela facilement en glissant une règle le long de la courbe).
On en déduit que la vitesse de croissance est maximale vers le 80
. (On peut voir cela facilement en glissant une règle le long de la courbe).
On en déduit que la vitesse de croissance est maximale vers le 80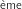 jour, le maïs ayant une hauteur d'environ 1,10 m.
jour, le maïs ayant une hauteur d'environ 1,10 m.
 correspond à la vitesse de croissance.
Par observation graphique ce coefficient est maximum autour de
correspond à la vitesse de croissance.
Par observation graphique ce coefficient est maximum autour de 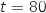 . (On peut voir cela facilement en glissant une règle le long de la courbe).
On en déduit que la vitesse de croissance est maximale vers le 80
. (On peut voir cela facilement en glissant une règle le long de la courbe).
On en déduit que la vitesse de croissance est maximale vers le 80 jour, le maïs ayant une hauteur d'environ 1,10 m.
jour, le maïs ayant une hauteur d'environ 1,10 m.
