Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2013 en Polynésie
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples. Aucune justification n'est demandée. Pour chacune des questions, une seule des quatres propositions est exacte. Chaque réponse correcte rapporte un point. Une réponse erronnée ou une absence de réponse n'ôte pas de point. Le candidat indiquera sur la copie le numéro de la question et la réponse choisie.
1. Soit
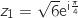et 
.
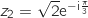La forme exponentielle de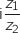 
est :
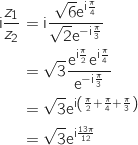La bonne réponse est la réponse d.
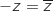, d'inconnue complexe 
admet :
a. une solution
b. deux solutions
c. une infinité de solutions dont les points images dans le plan complexe sont situés sur une droite
d. une infinité de solutions dont les points images dans le plan complexe sont situés sur un cercle.
Pour résoudre cette équation on écrit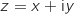 
où 
et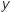 
sont des nombres réels.
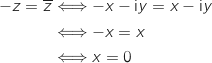Donc l'ensemble des solutions est l'ensemble des nombres complexes dont la partie réelle est nulle c'est à dire l'ensemble des imaginaires purs.
La bonne réponse est la réponse c.
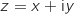où et 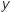sont des nombres réels.
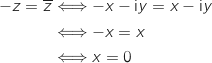Donc l'ensemble des solutions est l'ensemble des nombres complexes dont la partie réelle est nulle c'est à dire l'ensemble des imaginaires purs.
La bonne réponse est la réponse c.
3. Dans un repère orthonormé de l'espace, on considère les trois points A
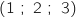, B
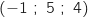et C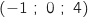
.
La droite parallèle à la droite (AB) passant par le point C a pour représentation paramétrique :
Un vecteur directeur de la droite (AB) est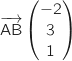 
.
Comme la droite considérée passe par C, un représentation paramétrique s'obtient directement :
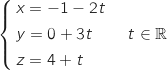La bonne réponse est la réponse a.
4. Dans un repère orthonormé de l'espace, on considère le plan .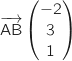
Comme la droite considérée passe par C, un représentation paramétrique s'obtient directement :
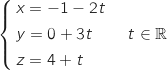La bonne réponse est la réponse a.
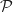passant par le point D
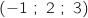et
de vecteur normal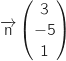 
, et la droite 
de représentation paramétrique
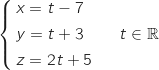a. La droite est perpendiculaire au plan .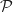
b. La droite est parallèle au plan 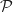et n'a pas de point commun avec le plan .
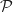c. La droite et le plan 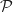sont sécants.
d. La droite est incluse dans le plan .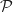
Un vecteur directeur de se lit directement sur la représentation paramétrique : 
.
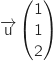On remarque déjà que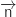 
et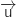 
ne sont pas colinéaires ce qui exclu la réponse a.
Le produit scalaire des deux vecteurs donne :
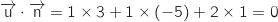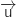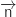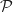Ainsi et sont orthogonaux ce qui montre que est parallèle à , donc la bonne
réponse peut être b. ou d. Pour trancher on regarde si la droite est incluse dans .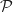
En utilisant le vecteur normal de 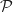on peut dire qu'une équation cartésienne du plan est de la forme :
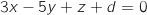Comme D
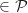on a :
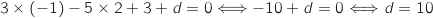Du coup une équation de 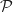est :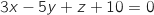 
.
Les coordonnées des points de sont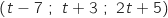 
lorsque 
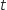décrit 
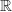. On teste si ces points vérifient l'équation de :
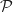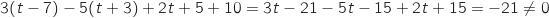Donc la droite n'est pas incluse dans .
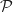La bonne réponse est la réponse b.
se lit directement sur la représentation paramétrique : .
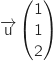On remarque déjà que 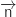et 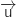ne sont pas colinéaires ce qui exclu la réponse a.
Le produit scalaire des deux vecteurs donne :
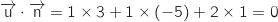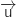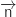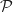Ainsi et sont orthogonaux ce qui montre que est parallèle à , donc la bonne
réponse peut être b. ou d. Pour trancher on regarde si la droite est incluse dans .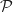
En utilisant le vecteur normal de 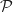on peut dire qu'une équation cartésienne du plan est de la forme :
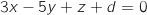Comme D 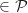on a :
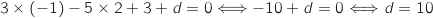Du coup une équation de 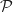est : .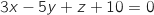
Les coordonnées des points de sont 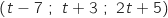lorsque 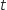décrit 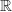. On teste si ces points vérifient l'équation de :
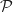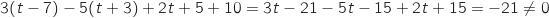Donc la droite n'est pas incluse dans .
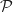La bonne réponse est la réponse b.
