Sujet et corrigé de l'exercice 1 du bac S de maths de juin 2013 en Polynésie
Cacher les corrigés
On considère la fonction définie sur
définie sur 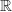 par
par 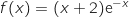 .
On note
.
On note  la courbe représentative de la
fonction
la courbe représentative de la
fonction  dans un repère orthogonal.
dans un repère orthogonal.
1. Etude de la fonction
 .
a. Déterminer les coordonnées des points d'intersection de la courbe
.
a. Déterminer les coordonnées des points d'intersection de la courbe  avec les axes du repère.
avec les axes du repère.
Axe des abscisses
On résout l'équation :
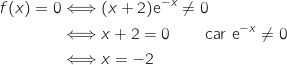 Donc
Donc  coupe l'axe des abscisses en
coupe l'axe des abscisses en 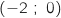 .
Axe des ordonnées
Il suffit de calculer
.
Axe des ordonnées
Il suffit de calculer 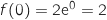 .
Donc
.
Donc  coupe l'axe des ordonnées en
coupe l'axe des ordonnées en 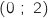 .
.
b. Etudier les limites de la fonction 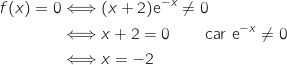 Donc
Donc  coupe l'axe des abscisses en
coupe l'axe des abscisses en 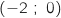 .
Axe des ordonnées
Il suffit de calculer
.
Axe des ordonnées
Il suffit de calculer 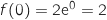 .
Donc
.
Donc  coupe l'axe des ordonnées en
coupe l'axe des ordonnées en 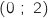 .
.
 en
en 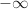 et en
et en  .
En déduire les éventuelles asymptotes à la courbe
.
En déduire les éventuelles asymptotes à la courbe  .
.
Limite en 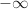
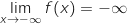 .
Limite en
.
Limite en  On est en présence d'une forme indéterminée et on écrit :
On est en présence d'une forme indéterminée et on écrit :
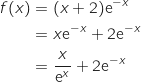
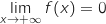 .
Ce résultat de limite permet de dire que la courbe
.
Ce résultat de limite permet de dire que la courbe  admet comme asymptote l'axe des abscisses en
admet comme asymptote l'axe des abscisses en  .
.
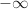
-
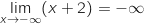
-
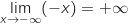 et par composition
et par composition
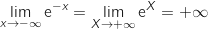
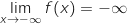 .
Limite en
.
Limite en  On est en présence d'une forme indéterminée et on écrit :
On est en présence d'une forme indéterminée et on écrit :
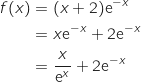
-
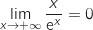 (limite connue)
(limite connue)
-
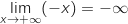 et par composée
et par composée
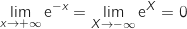 ;
en multipliant par 2 :
;
en multipliant par 2 :
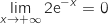
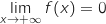 .
Ce résultat de limite permet de dire que la courbe
.
Ce résultat de limite permet de dire que la courbe  admet comme asymptote l'axe des abscisses en
admet comme asymptote l'axe des abscisses en  .
.
c. Etudier les variations de la fonction
 sur
sur 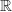 .
.
La fonction  est dérivable sur
est dérivable sur 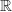 et on a en utilisant la relation de la dérivée d'un produit :
et on a en utilisant la relation de la dérivée d'un produit :
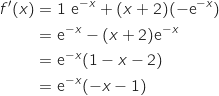 Comme pour tout
Comme pour tout 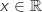 ,
, 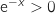 , le signe de
, le signe de 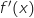 est le même que celui de
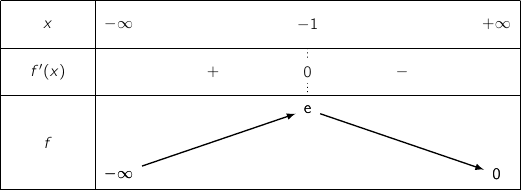
est le même que celui de 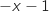 ce qui donne le tableau de
variations :
ce qui donne le tableau de
variations :
2. Calcul d'une valeur approchée de l'aire sous une courbe.
On note  est dérivable sur
est dérivable sur  et on a en utilisant la relation de la dérivée d'un produit :
et on a en utilisant la relation de la dérivée d'un produit :
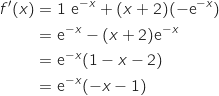 Comme pour tout
Comme pour tout 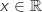 ,
, 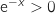 , le signe de
, le signe de 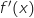 est le même que celui de
est le même que celui de 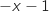 ce qui donne le tableau de
variations :
ce qui donne le tableau de
variations :

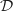 le domaine compris entre l'axe des abscisses, la courbe
le domaine compris entre l'axe des abscisses, la courbe  et les droites d'équation
et les droites d'équation 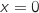 et
et 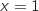 .
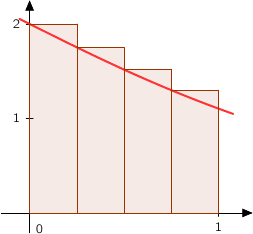
On approche l'aire du domaine
.
On approche l'aire du domaine 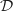 en calculant une somme d'aires de rectangles.
a. Dans cette question, on découpe l'intervalle
en calculant une somme d'aires de rectangles.
a. Dans cette question, on découpe l'intervalle 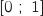 en quatre intervalles de même longueur :
en quatre intervalles de même longueur :
- sur l'intervalle
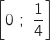 , on construit un rectangle de hauteur
, on construit un rectangle de hauteur 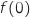
- sur l'intervalle
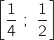 , on construit un rectangle de hauteur
, on construit un rectangle de hauteur 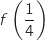
- sur l'intervalle
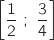 , on construit un rectangle de hauteur
, on construit un rectangle de hauteur 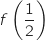
- sur l'intervalle
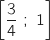 on construit un rectangle de hauteur
on construit un rectangle de hauteur 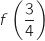 .
.
 en ajoutant les aires des quatre rectangles précédents :
en ajoutant les aires des quatre rectangles précédents :

 près du résultat affiché par cet algorithme.
près du résultat affiché par cet algorithme.
L'algorithme présenté calcule la somme des aires des rectangles considérés c'est à dire :
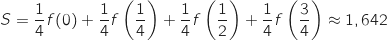
b. Dans cette question, 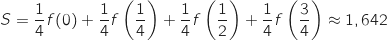
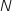 est un nombre entier strictement supérieur à 1.
On découpe l'intervalle
est un nombre entier strictement supérieur à 1.
On découpe l'intervalle 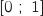 en
en 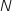 intervalles de même longueur.
Sur chacun de ces intervalles, on construit un rectangle en procédant de la même manière qu'à la question 2.a.
Modifier l'algorithme précédent afin qu'il affiche en sortie la somme des aires des
intervalles de même longueur.
Sur chacun de ces intervalles, on construit un rectangle en procédant de la même manière qu'à la question 2.a.
Modifier l'algorithme précédent afin qu'il affiche en sortie la somme des aires des 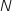 rectangles ainsi construits.
rectangles ainsi construits.
En découpant en 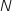 intervalles chaque intervalle a une longueur de
intervalles chaque intervalle a une longueur de 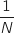 et on fait varier
et on fait varier 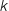 de 0 à
de 0 à 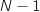 ce qui donne l'algorithme :
ce qui donne l'algorithme :

3. Calcul de la valeur exacte de l'aire sous une courbe.
Soit 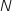 intervalles chaque intervalle a une longueur de
intervalles chaque intervalle a une longueur de 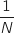 et on fait varier
et on fait varier 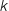 de 0 à
de 0 à 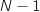 ce qui donne l'algorithme :
ce qui donne l'algorithme :

 la fonction définie sur
la fonction définie sur 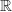 par
par 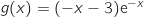 . On admet que la fonction
. On admet que la fonction  est une primitive de la fonction
est une primitive de la fonction  sur
sur 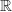 .
a. Calculer l'aire exacte
.
a. Calculer l'aire exacte 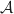 du domaine
du domaine 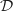 , exprimée en unités d'aire.
, exprimée en unités d'aire.
On remarque, par lecture du tableau de variations, que sur 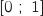 ,
, 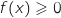 , donc l'aire du domaine
, donc l'aire du domaine 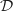 en unités d'aire s'obtient en
calculant :
en unités d'aire s'obtient en
calculant :
b. Donner une valeur approchée à  ,
, 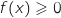 , donc l'aire du domaine
, donc l'aire du domaine 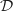 en unités d'aire s'obtient en
calculant :
en unités d'aire s'obtient en
calculant :
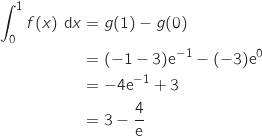
 près de l'erreur commise en remplaçant
près de l'erreur commise en remplaçant 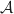 par la valeur approchée trouvée au moyen de l'algorithme à la question 2.a,
c'est-à-dire de l'écart entre ces deux valeurs.
par la valeur approchée trouvée au moyen de l'algorithme à la question 2.a,
c'est-à-dire de l'écart entre ces deux valeurs.
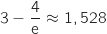 à
à  près.
L'erreur commise à
près.
L'erreur commise à  près vaut
près vaut 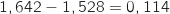 .
.
