Sujet et corrigé de l'exercice de spécialité du bac S de maths de mai 2013 au Liban
Cacher les corrigés
On considère la suite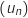 définie par
définie par 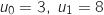 et, pour tout
et, pour tout  supérieur ou égal à 0 :
supérieur ou égal à 0 :
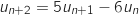
1. Calculer
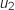 et
et 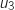 .
.
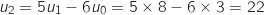
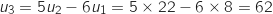
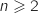 , on souhaite calculer
, on souhaite calculer 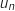 à l'aide de l'algorithme suivant :
à l'aide de l'algorithme suivant :

La ligne à compléter doit comporter la relation permettant de calculer le terme suivant de la suite en utilisant la relation de récurrence avec 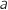 qui
représente
qui
représente 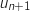 et
et  qui représente
qui représente 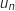 , du coup on écrit :
, du coup on écrit :
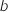 prend la valeur
prend la valeur 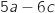 Comme
Comme 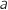 et
et 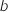 coïncident à ce niveau de l'algorithme on peut aussi écrire :
coïncident à ce niveau de l'algorithme on peut aussi écrire :
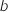 prend la valeur
prend la valeur 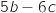 .
.
On obtient avec cet algorithme le tableau de valeurs suivant:
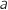 qui
représente
qui
représente 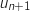 et
et  qui représente
qui représente 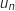 , du coup on écrit :
, du coup on écrit :
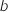 prend la valeur
prend la valeur 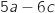 Comme
Comme 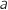 et
et 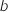 coïncident à ce niveau de l'algorithme on peut aussi écrire :
coïncident à ce niveau de l'algorithme on peut aussi écrire :
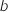 prend la valeur
prend la valeur 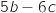 .
.
 b. Quelle conjecture peut-on émettre concernant la monotonie de la suite
b. Quelle conjecture peut-on émettre concernant la monotonie de la suite 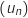 ?
?
On conjecture que 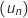 est strictement croissante et qu'elle diverge vers
est strictement croissante et qu'elle diverge vers  .
.
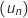 est strictement croissante et qu'elle diverge vers
est strictement croissante et qu'elle diverge vers  .
.
3. Pour tout entier naturel
 , on note
, on note 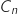 la matrice colonne
la matrice colonne 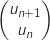 .
On note A la matrice carrée d'ordre 2 telle que, pour tout entier naturel
.
On note A la matrice carrée d'ordre 2 telle que, pour tout entier naturel  ,
,
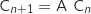 .
Déterminer A et prouver que, pour tout entier naturel
.
Déterminer A et prouver que, pour tout entier naturel 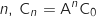 .
.
On doit compléter le calcul suivant :
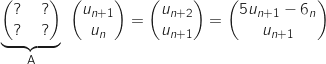 Pour que le calcul « fonctionne » il faut prendre
Pour que le calcul « fonctionne » il faut prendre 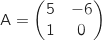 .
On montre par récurrence que pour tout entier naturel
.
On montre par récurrence que pour tout entier naturel  , la propriété
, la propriété 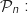 «
« 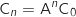 » est vraie.
Initialisation au rang 0
» est vraie.
Initialisation au rang 0
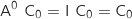 , donc
, donc 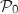 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 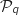 est vraie c'est à dire qu'on suppose avoir :
est vraie c'est à dire qu'on suppose avoir : 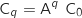 .
On montre qu'alors
.
On montre qu'alors 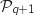 est également vraie.
est également vraie.
 Donc
Donc 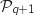 est vraie.
Ainsi la propriété est initialisée au rang 0 ; elle est héréditaire donc elle est vraie pour tout entier naturel.
est vraie.
Ainsi la propriété est initialisée au rang 0 ; elle est héréditaire donc elle est vraie pour tout entier naturel.
4. Soient 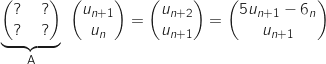 Pour que le calcul « fonctionne » il faut prendre
Pour que le calcul « fonctionne » il faut prendre 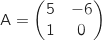 .
On montre par récurrence que pour tout entier naturel
.
On montre par récurrence que pour tout entier naturel  , la propriété
, la propriété 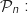 «
« 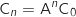 » est vraie.
Initialisation au rang 0
» est vraie.
Initialisation au rang 0
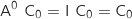 , donc
, donc 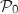 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 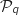 est vraie c'est à dire qu'on suppose avoir :
est vraie c'est à dire qu'on suppose avoir : 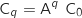 .
On montre qu'alors
.
On montre qu'alors 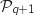 est également vraie.
est également vraie.
 Donc
Donc 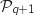 est vraie.
Ainsi la propriété est initialisée au rang 0 ; elle est héréditaire donc elle est vraie pour tout entier naturel.
est vraie.
Ainsi la propriété est initialisée au rang 0 ; elle est héréditaire donc elle est vraie pour tout entier naturel.

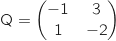 .
Calculer
.
Calculer 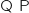 .
On admet que
.
On admet que 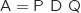 .
Démontrer par récurrence que, pour tout entier naturel non nul
.
Démontrer par récurrence que, pour tout entier naturel non nul 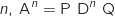 .
.
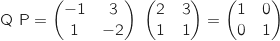 On peut donc dire que Q et P sont des matrices inverses l'une de l'autre.
Cette fois la propriété à montrer par récurrence pour tout entier
On peut donc dire que Q et P sont des matrices inverses l'une de l'autre.
Cette fois la propriété à montrer par récurrence pour tout entier 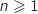 est :
est :
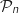 : «
: « 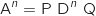 ».
Initialisation au rang 1
On admet que
».
Initialisation au rang 1
On admet que 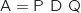 donc
donc 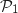 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 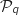 est vraie avec
est vraie avec 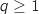 c'est à dire qu'on a l'hypothèse de récurrence :
c'est à dire qu'on a l'hypothèse de récurrence :
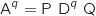
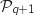 est également vraie.
est également vraie.
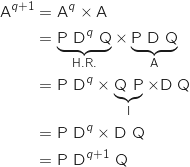 Donc
Donc 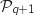 est vraie.
Ainsi la propriété
est vraie.
Ainsi la propriété 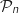 est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel
est vraie au rang 1 et est héréditaire donc elle est vraie pour tout entier naturel 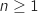 .
.
 ,
,
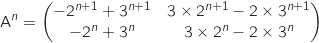
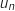 en fonction de
en fonction de  .
La suite
.
La suite 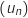 a-t-elle une limite ?
a-t-elle une limite ?
On a 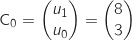 et on a
et on a
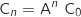 que l'on calcule :
que l'on calcule :
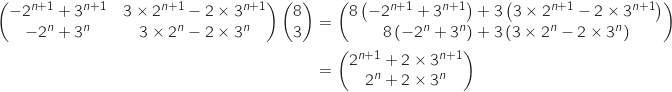 Donc
Donc 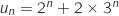 .
.
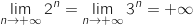 car
car 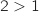 et
et 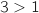 .
Donc
.
Donc 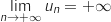 ce qui signifie que la suite
ce qui signifie que la suite 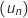 diverge vers
diverge vers  .
.
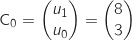 et on a
et on a
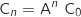 que l'on calcule :
que l'on calcule :
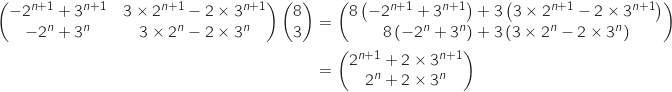 Donc
Donc 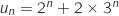 .
.
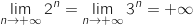 car
car 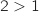 et
et 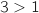 .
Donc
.
Donc 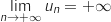 ce qui signifie que la suite
ce qui signifie que la suite 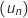 diverge vers
diverge vers  .
.
