Corrigé de l'exercice 3 du bac S de maths de mai 2012 au Liban
Cacher les corrigés
On dispose de deux urnes U
et U
.
L'urne U contient 4 jetons numérotés de 1 à 4.
L'urne U contient 4 boules blanches et 6 boules noires.
Un jeu consiste à tirer un jeton de l'urne U, à noter son numéro, puis à tirer simultanément de l'urne U le nombre de boules indiqué par le jeton.
On considère les événements suivants:
- J : « le jeton tiré de l'urne U porte le numéro 1 »
- J : « le jeton tiré de l'urne U porte le numéro 2 »
- J
: « le jeton tiré de l'urne U porte le numéro 3 »
- J
: « le jeton tiré de l'urne U porte le numéro 4 »
- B : « toutes les boules tirées de l'urne U sont blanches»
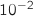suffit.
1. Calculer
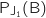, probabilité de l'événement B sachant que l'événement J est réalisé.
Si le joueur tire le jeton avec le numéro 1, il tire ensuite une boule parmi 10 dans l'urne U, donc la probabilité qu'il tire une boule blanche est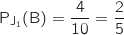 
.
On admet dans la suite les résultats suivants:
, donc la probabilité qu'il tire une boule blanche est .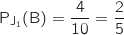
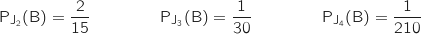
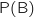, probabilité de l'événement B, vaut 
.
On pourra s'aider d'un arbre de probabilités.
On peut déjà remarquer que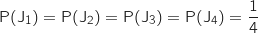 
(tirage d'un jeton parmi 4 dans une situation d'équiprobabilité).
Les événements J, J, J et J constituent un système complet d'événements, donc d'après la formule des probabilités totales :
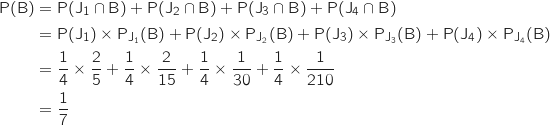
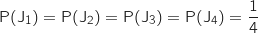(tirage d'un jeton parmi 4 dans une situation d'équiprobabilité).
Les événements J, J, J et J constituent un système complet d'événements, donc d'après la formule des probabilités totales :
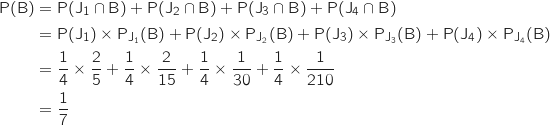
3. On dit à un joueur que toutes les boules qu'il a tirées sont blanches. Quelle est la probabilité que le jeton tiré porte le numéro 3?
Il s'agit de calculer :
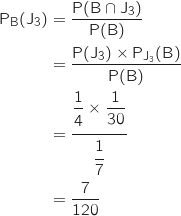
4. On joue 10 fois de suite à ce jeu. Chacune des parties est indépendante des précédentes. On note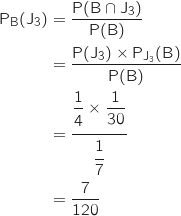
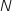la variable aléatoire prenant comme valeur le nombre de parties où toutes les boules tirées sont blanches.
a. Quelle est la loi suivie par la variable aléatoire ?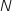
On répète 10 fois de façon indépendante une expérience de Bernoulli dont la probabilité du succès (obtenir que des boules blanches) est .
La variable aléatoire 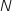qui compte le nombre de succès, c'est à dire le nombre de parties où toutes les boules tirées sont blanches suit une loi binomiale 
.
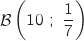b. Calculer la probabilité de l'événement .
La variable aléatoire 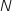qui compte le nombre de succès, c'est à dire le nombre de parties où toutes les boules tirées sont blanches suit une loi binomiale .
.
.
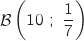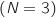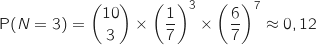