Corrigé de l'exercice 1 du bac S de maths de mai 2012 au Liban
Cacher les corrigés
Partie A
On considère la fonction définie sur l'intervalle
définie sur l'intervalle 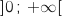 par:
par:
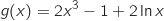
 sur l'intervalle
sur l'intervalle 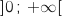 .
.
La fonction  est définie et dérivable sur
est définie et dérivable sur 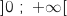 et pour tout nombre réel
et pour tout nombre réel  de cet intervalle on a :
de cet intervalle on a :
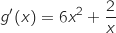
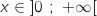 ,
, 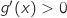 , donc la fonction
, donc la fonction  est strictement croissante sur
est strictement croissante sur 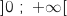 .
.
 est définie et dérivable sur
est définie et dérivable sur 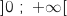 et pour tout nombre réel
et pour tout nombre réel  de cet intervalle on a :
de cet intervalle on a :
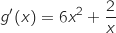
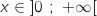 ,
, 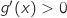 , donc la fonction
, donc la fonction  est strictement croissante sur
est strictement croissante sur 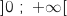 .
.
2. Justifier qu'il existe un unique réel
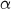 tel que
tel que 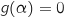 .
Donner une valeur approchée de
.
Donner une valeur approchée de 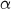 , arrondir au centième.
, arrondir au centième.
On commence par calculer les limites à droite en 0 et en  de la fonction
de la fonction  .
Limite à droite en 0
.
Limite à droite en 0
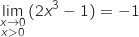
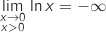 et par produit
et par produit 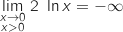 .
Finalement, par somme
.
Finalement, par somme 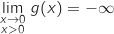 .
Limite en
.
Limite en 
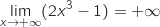
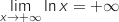 et par produit
et par produit 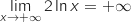 Finalement par addition,
Finalement par addition, 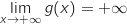 .
Ainsi la fonction
.
Ainsi la fonction  est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur 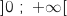 avec :
avec :
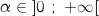 tel que
tel que 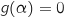 .
.
Avec la calculette on trouve 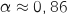 .
.
 de la fonction
de la fonction  .
Limite à droite en 0
.
Limite à droite en 0
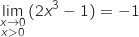
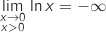 et par produit
et par produit 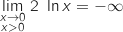 .
Finalement, par somme
.
Finalement, par somme 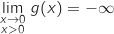 .
Limite en
.
Limite en 
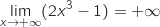
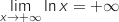 et par produit
et par produit 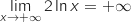 Finalement par addition,
Finalement par addition, 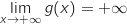 .
Ainsi la fonction
.
Ainsi la fonction  est définie, continue et strictement croissante sur
est définie, continue et strictement croissante sur 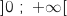 avec :
avec :
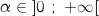 tel que
tel que 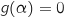 .
.

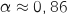 .
.
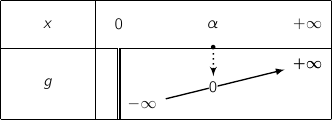
3. En déduire le signe de la fonction
 sur l'intervalle
sur l'intervalle 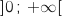 .
.
En utilisant ce qui précède on a directement le tableau de signes :


Partie B
On considère la fonction définie sur l'intervalle
définie sur l'intervalle 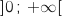 par :
par :
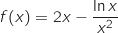
 la courbe représentative de la fonction
la courbe représentative de la fonction  dans le plan, muni d'un repère orthogonal
dans le plan, muni d'un repère orthogonal 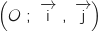 .
1. Déterminer les limites de la fonction
.
1. Déterminer les limites de la fonction  en
en 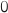 et en
et en  .
.
Limite à droite en 0
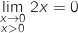
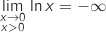 et
et 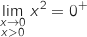 donc
par quotient
donc
par quotient 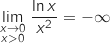 .
Finalement par soustraction
.
Finalement par soustraction 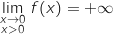 .
Limite en
.
Limite en 
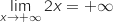
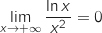 (limite de référence).
Finalement par soustraction
(limite de référence).
Finalement par soustraction 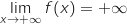 .
.
2. On considère la droite 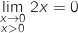
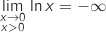 et
et 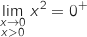 donc
par quotient
donc
par quotient 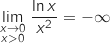 .
Finalement par soustraction
.
Finalement par soustraction 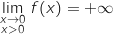 .
Limite en
.
Limite en 
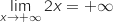
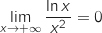 (limite de référence).
Finalement par soustraction
(limite de référence).
Finalement par soustraction 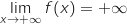 .
.
 d'équation
d'équation 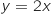 .
Etudier la position relative de la courbe
.
Etudier la position relative de la courbe 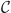 et de la droite
et de la droite  .
.
Dans le sujet original il faut établir que  est asymptote oblique à la courbe
est asymptote oblique à la courbe  .
Depuis la rentrée 2012, la notion d'asymptote oblique n'est plus au programme.
.
Depuis la rentrée 2012, la notion d'asymptote oblique n'est plus au programme.
 est asymptote oblique à la courbe
est asymptote oblique à la courbe  .
Depuis la rentrée 2012, la notion d'asymptote oblique n'est plus au programme.
.
Depuis la rentrée 2012, la notion d'asymptote oblique n'est plus au programme.
Pour tout 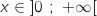 , on considère l'expression :
, on considère l'expression : 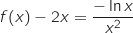 .
Pour étudier la position relative de
.
Pour étudier la position relative de  et
et  on étudie le signe de
on étudie le signe de 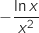 .
Le signe est le même que celui de
.
Le signe est le même que celui de 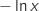 , on a donc le tableau de signes :
, on a donc le tableau de signes :
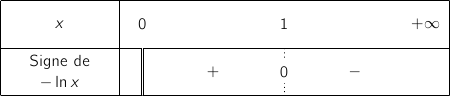
On en déduit que :
3. Justifier que 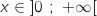 , on considère l'expression :
, on considère l'expression : 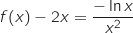 .
Pour étudier la position relative de
.
Pour étudier la position relative de  et
et  on étudie le signe de
on étudie le signe de 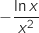 .
Le signe est le même que celui de
.
Le signe est le même que celui de 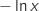 , on a donc le tableau de signes :
, on a donc le tableau de signes :

-
 est au dessus de
est au dessus de  pour
pour 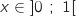 ,
,
-
 et
et  se coupent pour
se coupent pour 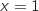 ,
,
-
 est en dessous de
est en dessous de  pour
pour 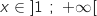 .
.
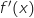 a même signe que
a même signe que 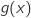 .
.
La fonction  est dérivable sur
est dérivable sur 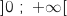 et on a :
et on a :
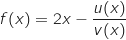 avec :
avec :
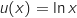
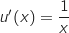
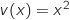
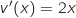 Donc
Donc 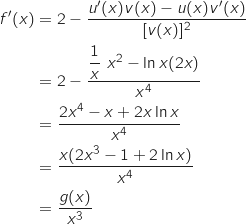 Comme
Comme 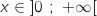 , le signe de
, le signe de 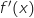 est le même que celui de
est le même que celui de 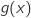 .
.
4. En déduire le tableau de variation de la fonction  est dérivable sur
est dérivable sur 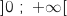 et on a :
et on a :
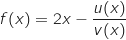 avec :
avec :
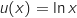
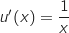
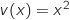
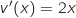 Donc
Donc 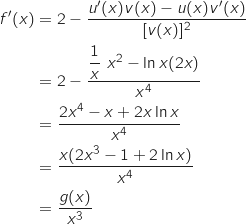 Comme
Comme 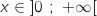 , le signe de
, le signe de 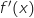 est le même que celui de
est le même que celui de 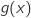 .
.
 .
.
On a le tableau de variations :
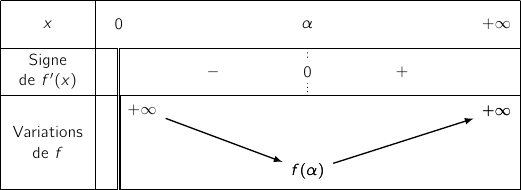
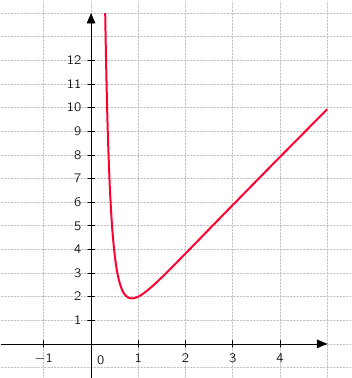
5. Tracer la courbe 
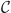 dans le repère
dans le repère 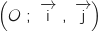 . On prendra comme unités: 2 cm sur l'axe des abscisses, 1 cm sur l'axe des ordonnées.
. On prendra comme unités: 2 cm sur l'axe des abscisses, 1 cm sur l'axe des ordonnées.
Partie C
Soit un entier naturel non nul. On considère l'aire du domaine
un entier naturel non nul. On considère l'aire du domaine 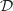 du plan compris entre la courbe
du plan compris entre la courbe 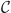 , la droite
, la droite  et les droites d'équations respectives
et les droites d'équations respectives 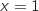 et
et 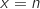 .
1. Justifier que cette aire, exprimée en cm
.
1. Justifier que cette aire, exprimée en cm , est donnée par:
, est donnée par:
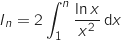
Sur l'intervalle 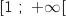 , on a vu que la droite
, on a vu que la droite  est située au dessus de
est située au dessus de  , donc l'aire
du domaine
, donc l'aire
du domaine 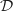 en unités d'aire s'obtient en calculant l'intégrale :
en unités d'aire s'obtient en calculant l'intégrale :
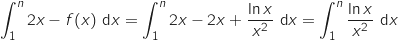 où pour tout entier
où pour tout entier 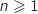 , la fonction
, la fonction 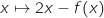 est définie et continue sur
est définie et continue sur 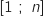 .
L'unité d'aire vaut 2 cm
.
L'unité d'aire vaut 2 cm donc l'aire de
donc l'aire de 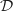 exprimée en cm
exprimée en cm est donnée par :
est donnée par :
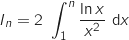
2.a. On admet que 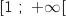 , on a vu que la droite
, on a vu que la droite  est située au dessus de
est située au dessus de  , donc l'aire
du domaine
, donc l'aire
du domaine 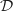 en unités d'aire s'obtient en calculant l'intégrale :
en unités d'aire s'obtient en calculant l'intégrale :
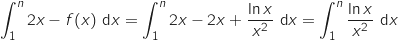 où pour tout entier
où pour tout entier 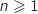 , la fonction
, la fonction 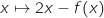 est définie et continue sur
est définie et continue sur 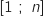 .
L'unité d'aire vaut 2 cm
.
L'unité d'aire vaut 2 cm donc l'aire de
donc l'aire de 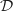 exprimée en cm
exprimée en cm est donnée par :
est donnée par :
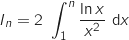
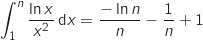 .
.
Dans le sujet original il faut calculer cette intégrale en utilisant une intégration par parties.
A partir de la session 2013 du baccalauréat, la méthode d'intégration par parties ne figure plus au programme.
b. En déduire l'expression de 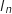 en fonction de
en fonction de  .
.
Il suffit de multiplier par 2 le résultat précédent :
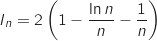 .
.
3. Calculer la limite de l'aire 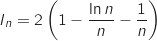 .
.
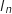 du domaine
du domaine 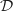 quand
quand  tend vers
tend vers  .
.
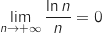 (limite de référence)
(limite de référence)
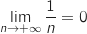 Donc
Donc 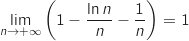 .
Et finalement, par produit :
.
Et finalement, par produit : 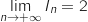 .
.
