Corrigé de l'exercice 2 du bac S de maths de juin 2012 dans les centres étrangers
Cacher les corrigés
On considère la suite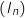 définie pour
définie pour  entier naturel non nul par :
entier naturel non nul par :
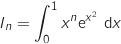
 la fonction définie sur
la fonction définie sur 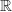 par
par 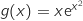 .
Démonter que la fonction
.
Démonter que la fonction 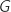 définie sur
définie sur 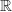 par
par 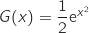 est une primitive sur
est une primitive sur 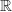 de la fonction
de la fonction  .
.
La fonction 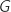 proposée est définie et dérivable sur
proposée est définie et dérivable sur 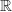 et en utilisant la formule de dérivation d'une composée :
et en utilisant la formule de dérivation d'une composée :
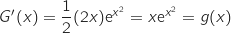 Donc
Donc 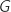 est bien une primitive de
est bien une primitive de  .
.
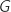 proposée est définie et dérivable sur
proposée est définie et dérivable sur 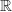 et en utilisant la formule de dérivation d'une composée :
et en utilisant la formule de dérivation d'une composée :
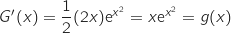 Donc
Donc 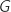 est bien une primitive de
est bien une primitive de  .
.
b. En déduire la valeur de
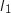 .
.
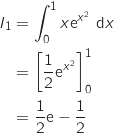
 , supérieur ou égal à 1, on a :
, supérieur ou égal à 1, on a :
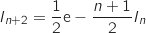
Dans le sujet original, les élèves doivent établir cette relation en utilisant une intégration par parties qui ne
figure plus au programme depuis la rentrée 2012.
d. Calculer
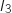 et
et 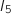 .
.
D'après la question précédente :
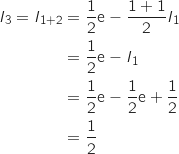
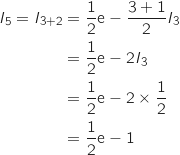
2. On considère l'algorithme suivant :
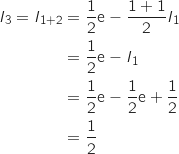
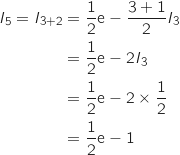

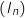 obtient-on en sortie de cet algorithme ?
obtient-on en sortie de cet algorithme ?
On entre la première fois dans le Tant que avec la valeur 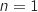 et on calcule
et on calcule 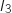 (en utilisant la relation de récurrence vue en 1.c.), à la deuxième itération
(en utilisant la relation de récurrence vue en 1.c.), à la deuxième itération 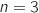 et on calcule
et on calcule 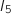 , ... , la dernière itération a lieu avec la valeur
, ... , la dernière itération a lieu avec la valeur 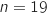 et on calcule
et on calcule 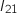 .
Donc on obtient
.
Donc on obtient 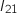 en sortie de cet algorithme.
en sortie de cet algorithme.
3.a. Montrer que, pour tout entier naturel non nul 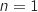 et on calcule
et on calcule 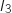 (en utilisant la relation de récurrence vue en 1.c.), à la deuxième itération
(en utilisant la relation de récurrence vue en 1.c.), à la deuxième itération 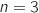 et on calcule
et on calcule 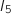 , ... , la dernière itération a lieu avec la valeur
, ... , la dernière itération a lieu avec la valeur 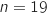 et on calcule
et on calcule 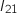 .
Donc on obtient
.
Donc on obtient 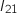 en sortie de cet algorithme.
en sortie de cet algorithme.
 ,
, 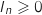 .
.
Pour tout 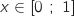 ,
, 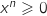 et
et  , donc
, donc 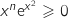 et l'intégrale aussi.
et l'intégrale aussi.
b. Montrer que la suite 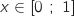 ,
, 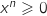 et
et  , donc
, donc 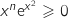 et l'intégrale aussi.
et l'intégrale aussi.
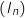 est décroissante.
est décroissante.
Pour tout entier 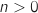 on a :
on a :
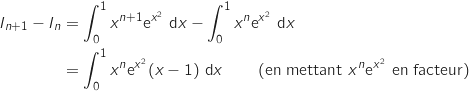 or, pour tout
or, pour tout 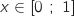 ,
, 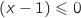 ,
, 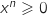 et
et 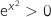 , du coup
, du coup 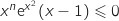 et l'intégrale est négative.
Par suite,
et l'intégrale est négative.
Par suite, 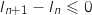 , ce qui montre que la suite
, ce qui montre que la suite 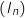 est décroissante.
est décroissante.
c. En déduire que la suite 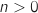 on a :
on a :
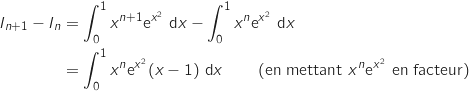 or, pour tout
or, pour tout 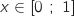 ,
, 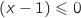 ,
, 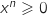 et
et 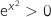 , du coup
, du coup 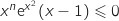 et l'intégrale est négative.
Par suite,
et l'intégrale est négative.
Par suite, 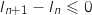 , ce qui montre que la suite
, ce qui montre que la suite 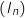 est décroissante.
est décroissante.
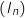 est convergente.
On note
est convergente.
On note 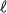 sa limite.
sa limite.
D'après ce qui précède la suite 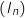 est minorée par 0 et elle est décroissante donc elle est convergente.
est minorée par 0 et elle est décroissante donc elle est convergente.
4. Dans cette question, toute trace de recherche même incomplète, ou d'initiative même non fructueuse, sera prise en compte dans l'évaluation.
Déterminer la valeur de 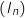 est minorée par 0 et elle est décroissante donc elle est convergente.
est minorée par 0 et elle est décroissante donc elle est convergente.
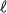 .
.
Pour tout 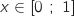 ,
, 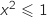 et
et 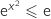 , comme sur cet intervalle,
, comme sur cet intervalle, 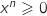 , on a
, on a 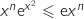 .
L'intégration de 0 à 1 conserve l'ordre ce qui donne :
.
L'intégration de 0 à 1 conserve l'ordre ce qui donne :
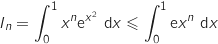 avec :
avec : 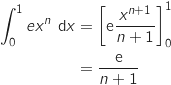 Ainsi pour tout entier
Ainsi pour tout entier 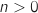 ,
, 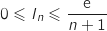 , avec
, avec 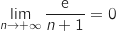 , donc d'après le théorème
des gendarmes, la suite
, donc d'après le théorème
des gendarmes, la suite 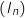 converge vers 0.
converge vers 0.
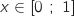 ,
, 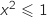 et
et 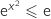 , comme sur cet intervalle,
, comme sur cet intervalle, 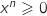 , on a
, on a 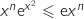 .
L'intégration de 0 à 1 conserve l'ordre ce qui donne :
.
L'intégration de 0 à 1 conserve l'ordre ce qui donne :
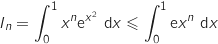 avec :
avec : 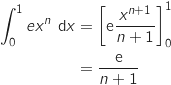 Ainsi pour tout entier
Ainsi pour tout entier 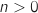 ,
, 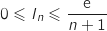 , avec
, avec 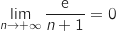 , donc d'après le théorème
des gendarmes, la suite
, donc d'après le théorème
des gendarmes, la suite 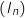 converge vers 0.
converge vers 0.
