Corrigé de l'exercice 4 du bac S de maths de juin 2012 en Asie
Cacher les corrigés
1. On considère l'algorithme suivant :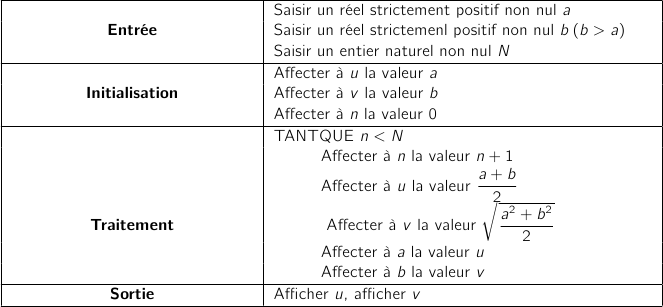
Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour
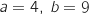 et
et 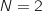 . Les valeurs successives de
. Les valeurs successives de  et
et  seront arrondies au millième.
seront arrondies au millième.


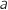 et
et 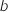 sont deux réels tels que
sont deux réels tels que 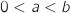 .
On considère les suites
.
On considère les suites 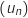 et
et 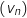 définies par
définies par
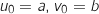 et pour tout entier naturel
et pour tout entier naturel  :
:
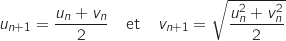
2.a. Démontrer par récurrence que, pour tout entier naturel
 , on a
, on a 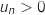 et
et 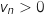 .
.
La propriété à montrer pour tout entier 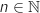 est :
est :
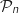 :
: 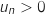 et
et 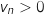 Initialisation au rang 0
On a
Initialisation au rang 0
On a 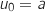 et
et 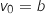 avec
avec 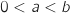 , donc
, donc  est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 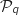 est vraie à un rang
est vraie à un rang 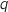 , c'est à dire qu'on a l'hypothèse de récurrence :
, c'est à dire qu'on a l'hypothèse de récurrence : 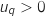 et
et 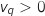 .
On cherche à montrer, qu'alors,
.
On cherche à montrer, qu'alors, 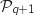 est vraie.
est vraie.
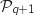 est vraie.
La propriété
est vraie.
La propriété 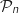 est initialisée au rang 0 et elle est héréditaire, donc elle est vraie pour tout entier naturel
est initialisée au rang 0 et elle est héréditaire, donc elle est vraie pour tout entier naturel  .
.
b. Démontrer que, pour tout entier naturel 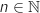 est :
est :
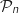 :
: 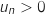 et
et 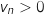 Initialisation au rang 0
On a
Initialisation au rang 0
On a 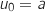 et
et 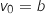 avec
avec 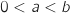 , donc
, donc 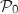 est vraie.
Hérédité
On suppose que
est vraie.
Hérédité
On suppose que 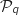 est vraie à un rang
est vraie à un rang 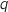 , c'est à dire qu'on a l'hypothèse de récurrence :
, c'est à dire qu'on a l'hypothèse de récurrence : 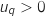 et
et 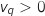 .
On cherche à montrer, qu'alors,
.
On cherche à montrer, qu'alors, 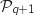 est vraie.
est vraie.
-
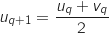 , or par hypothèse,
, or par hypothèse, 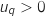 et
et 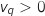 , donc
, donc 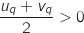 soit
soit 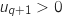 .
.
-
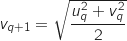 , or par hypothèse,
, or par hypothèse, 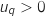 et
et 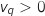 , donc
, donc 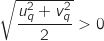 , soit
, soit 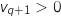 .
.
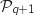 est vraie.
La propriété
est vraie.
La propriété 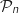 est initialisée au rang 0 et elle est héréditaire, donc elle est vraie pour tout entier naturel
est initialisée au rang 0 et elle est héréditaire, donc elle est vraie pour tout entier naturel  .
.
 :
: 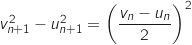 .
En déduire que, pour tout entier naturel
.
En déduire que, pour tout entier naturel  , on a
, on a 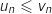 .
.
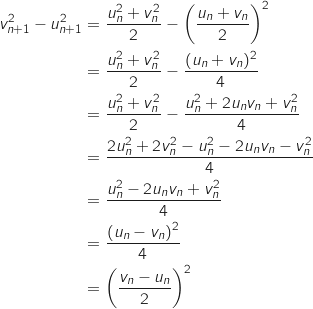 Donc pour tout entier naturel
Donc pour tout entier naturel  ,
, 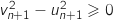 , soit
, soit 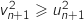 et comme
et comme
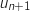 et
et 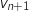 sont positifs on obtient
sont positifs on obtient 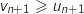 , ce qui entraîne que pour tout entier
, ce qui entraîne que pour tout entier 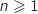 :
: 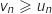 et comme
et comme 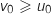 on a le résultat
pour tout entier naturel
on a le résultat
pour tout entier naturel  .
.
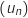 est croissante.
est croissante.
Pour tout entier naturel  , on a :
, on a :
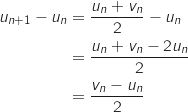 or pour tout
or pour tout 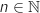 ,
, 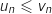 , donc
, donc 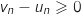 et du coup
et du coup 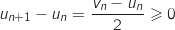 , c'est à dire que
, c'est à dire que 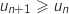 ou encore
que
ou encore
que 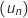 est croissante.
est croissante.
b. Comparer  , on a :
, on a :
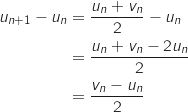 or pour tout
or pour tout 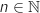 ,
, 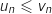 , donc
, donc 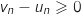 et du coup
et du coup 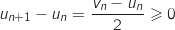 , c'est à dire que
, c'est à dire que 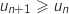 ou encore
que
ou encore
que 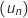 est croissante.
est croissante.
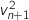 et
et 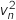 .
En déduire le sens de variation de la suite
.
En déduire le sens de variation de la suite 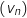 .
.
Pour tout entier naturel  :
:
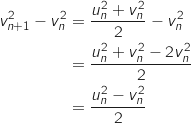 or pour tout entier naturel
or pour tout entier naturel  ,
, 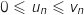 donc
donc 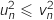 et du coup
et du coup 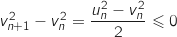 , soit
, soit
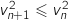 et comme
et comme 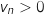 et
et 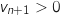 on en déduit que
on en déduit que 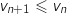 c'est à dire que
c'est à dire que 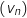 est décroissante.
est décroissante.
4. Justifier que pour tout entier naturel  :
:
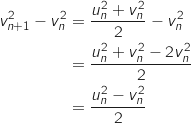 or pour tout entier naturel
or pour tout entier naturel  ,
, 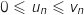 donc
donc 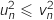 et du coup
et du coup 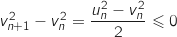 , soit
, soit
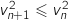 et comme
et comme 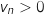 et
et 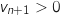 on en déduit que
on en déduit que 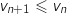 c'est à dire que
c'est à dire que 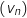 est décroissante.
est décroissante.
 ,
, 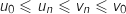 et en déduire que les suites
et en déduire que les suites 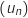 et
et 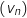 sont convergentes.
sont convergentes.
-
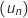 est croissante, donc elle est minorée par
est croissante, donc elle est minorée par 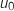 , soit
, soit 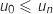 ,
,
-
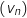 est décroissante, donc elle est majorée par
est décroissante, donc elle est majorée par 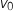 , soit
, soit 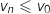 ,
,
- on a
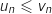
 , on a :
, on a : 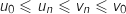 .
Ainsi la suite
.
Ainsi la suite 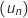 est croissante et majorée par
est croissante et majorée par 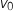 , donc elle est convergence d'après le théorème sur la convergence des suites monotones, de
même, la suite
, donc elle est convergence d'après le théorème sur la convergence des suites monotones, de
même, la suite 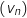 est décroissante et minorée par
est décroissante et minorée par 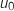 , donc elle est également convergente.
, donc elle est également convergente.
