Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2013 aux Antilles
Cacher les corrigés
Partie A
Soient un entier naturel,
un entier naturel, 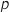 un nombre réel compris entre
un nombre réel compris entre 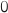 et
et 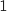 et
et 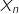 une variable aléatoire suivant une loi binomiale de paramètres
une variable aléatoire suivant une loi binomiale de paramètres  et
et 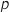 .
On note
.
On note 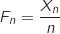 et
et  une valeur prise par
une valeur prise par 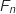 .
On rappelle que, pour
.
On rappelle que, pour  assez grand, l'intervalle
assez grand, l'intervalle 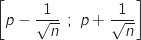 contient la fréquence
contient la fréquence  avec
une probabilité au moins égale à 0,95.
En déduire que l'intervalle
avec
une probabilité au moins égale à 0,95.
En déduire que l'intervalle 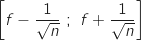 contient
contient 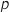 avec une probabilité au moins égale à 0,95.
avec une probabilité au moins égale à 0,95.
Pour  assez grand, avec une probabilité au moins égale à 0,95 on a :
assez grand, avec une probabilité au moins égale à 0,95 on a :
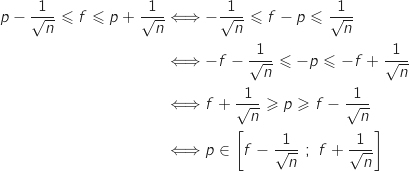
 assez grand, avec une probabilité au moins égale à 0,95 on a :
assez grand, avec une probabilité au moins égale à 0,95 on a :
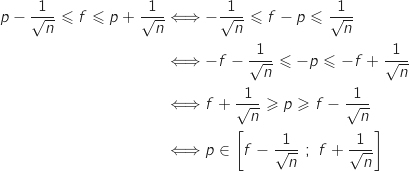
Partie B
On cherche à étudier le nombre d'étudiants connaissant la signification du sigle URSSAF. Pour cela, on les interroge en proposant un questionnaire à choix multiples. Chaque étudiant doit choisir parmi trois réponses possibles, notées A, B et C, la bonne réponse étant la A. On note la probabilité pour qu'un étudiant connaisse la bonne réponse. Tout étudiant connaissant la bonne réponse répond A, sinon il répond au hasard (de façon équiprobable).
On interroge un étudiant au hasard. On note :
la probabilité pour qu'un étudiant connaisse la bonne réponse. Tout étudiant connaissant la bonne réponse répond A, sinon il répond au hasard (de façon équiprobable).
On interroge un étudiant au hasard. On note :
- A l'événement « l'étudiant répond A »,
- B l'événement « l'étudiant répond B »,
- C l'événement « l'étudiant répond C »,
- R l'événement « l'étudiant connait la réponse »,
-
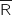 l'événement contraire de R.
l'événement contraire de R.
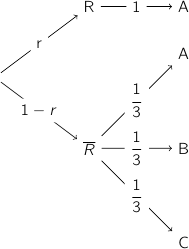
b. Montrer que la probabilité de l'événement A est
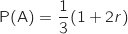 .
.
Les événements R et 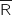 forment une partition de l'univers.
Avec la formule des probabilités totales on a :
forment une partition de l'univers.
Avec la formule des probabilités totales on a :
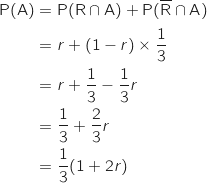
c. Exprimer en fonction de 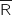 forment une partition de l'univers.
Avec la formule des probabilités totales on a :
forment une partition de l'univers.
Avec la formule des probabilités totales on a :
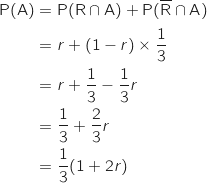
 la probabilité qu'une personne ayant choisi A connaisse la bonne réponse.
la probabilité qu'une personne ayant choisi A connaisse la bonne réponse.
Il s'agit de calculer : 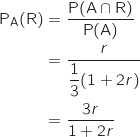
2. Pour estimer 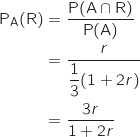
 , on interroge 400 personnes et on note
, on interroge 400 personnes et on note  la variable aléatoire comptant le nombre de bonnes réponses.
On admettra qu'interroger au hasard 400 étudiants revient à effectuer un tirage avec remise de 400 étudiants dans l'ensemble de tous les étudiants.
a. Donner la loi de
la variable aléatoire comptant le nombre de bonnes réponses.
On admettra qu'interroger au hasard 400 étudiants revient à effectuer un tirage avec remise de 400 étudiants dans l'ensemble de tous les étudiants.
a. Donner la loi de  et ses paramètres
et ses paramètres  et
et 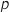 en fonction de
en fonction de  .
.
On répète de façon indépendante (tirage avec remise) 400 fois une même expérience de Bernoulli,
dont la probabilité du succès (une bonne réponse) est 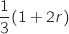 .
La variable aléatoire
.
La variable aléatoire  qui compte le nombre de bonnes réponses suit une loi
binomiale de paramètres :
qui compte le nombre de bonnes réponses suit une loi
binomiale de paramètres : 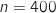 et
et 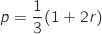 .
.
b. Dans un premier sondage, on constate que 240 étudiants répondent A, parmi les 400 interrogés.
Donner un intervalle de confiance au seuil de 95 % de l'estimation de 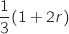 .
La variable aléatoire
.
La variable aléatoire  qui compte le nombre de bonnes réponses suit une loi
binomiale de paramètres :
qui compte le nombre de bonnes réponses suit une loi
binomiale de paramètres : 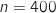 et
et 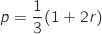 .
.
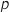 .
En déduire un intervalle de confiance au seuil de 95 % de
.
En déduire un intervalle de confiance au seuil de 95 % de  .
.
Un intervalle de confiance pour 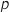 au seuil de 95 % est :
au seuil de 95 % est :
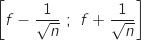
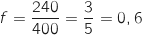 et
et 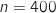 , ce qui donne :
, ce qui donne :
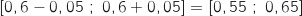 Et on a :
Et on a :
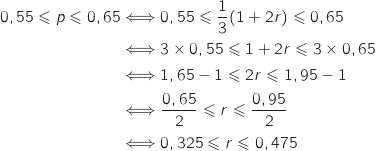 Donc un intervalle de confiance pour
Donc un intervalle de confiance pour  au seuil de 95 % est
au seuil de 95 % est 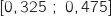 .
.
c. Dans la suite, on suppose que 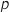 au seuil de 95 % est :
au seuil de 95 % est :
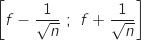
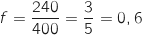 et
et 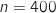 , ce qui donne :
, ce qui donne :
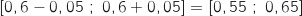 Et on a :
Et on a :
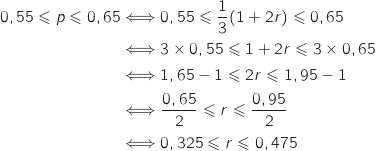 Donc un intervalle de confiance pour
Donc un intervalle de confiance pour  au seuil de 95 % est
au seuil de 95 % est 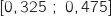 .
.
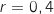 . Compte-tenu du grand nombre d'étudiants, on considérera que
. Compte-tenu du grand nombre d'étudiants, on considérera que  suit une loi normale.
i. Donner les paramètres de cette loi normale.
suit une loi normale.
i. Donner les paramètres de cette loi normale.
La variable aléatoire  considérée suit donc une loi binomiale de paramètre
considérée suit donc une loi binomiale de paramètre 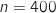 et
et
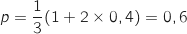 .
Son espérance est :
.
Son espérance est : 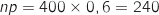 ;
son écart-type est :
;
son écart-type est :  .
Donc on peut considérer que
.
Donc on peut considérer que  suit une loi normale de paramétres
suit une loi normale de paramétres 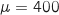 et
et 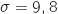 .
.
ii. Donner une valeur approchée de  considérée suit donc une loi binomiale de paramètre
considérée suit donc une loi binomiale de paramètre 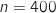 et
et
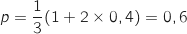 .
Son espérance est :
.
Son espérance est : 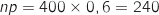 ;
son écart-type est :
;
son écart-type est :  .
Donc on peut considérer que
.
Donc on peut considérer que  suit une loi normale de paramétres
suit une loi normale de paramétres 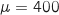 et
et 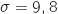 .
.
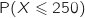 à
à 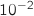 près.
On pourra s'aider de la table donnée ci-dessous, qui donne une valeur approchée de
près.
On pourra s'aider de la table donnée ci-dessous, qui donne une valeur approchée de 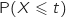 où
où  est la variable aléatoire de la question 2. c.
est la variable aléatoire de la question 2. c.
Par simple lecture dans le tableau donné on a :
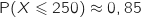
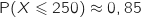
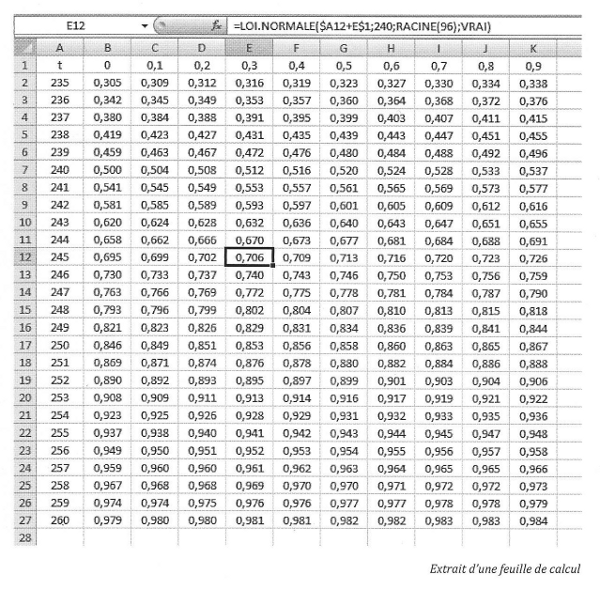
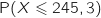 .
.
