Corrigé de l'exercice 2 du bac S de maths de juin 2012 aux Antilles
Cacher les corrigés
Le plan complexe est rapporté à un repère orthonormé direct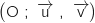
.
On réalisera sur une feuille de papier millimétré une figure en prenant pour unité 2 cm.
On complètera cette figure au fur et à mesure des questions.
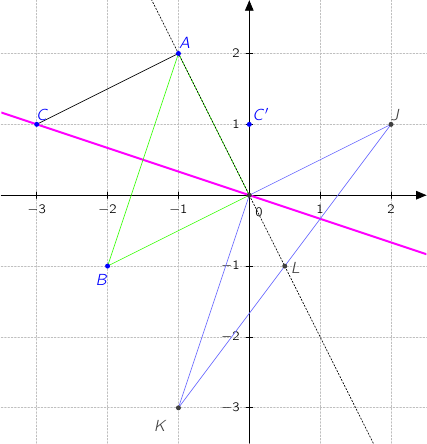
On considère les points A, B et C du plan complexe d'affixes respectives
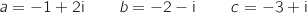
1. Placer les points A, B et C sur le graphique.
2. Calculer
, en déduire la nature du triangle OAB.
Du coup on a :
-
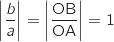, donc OB
OA, ce qui prouve que OAB est isocèle en O.
-
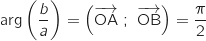, donc l'angle 
est droit et OAB est rectangle en O
qui à tout point 
d'affixe 
avec 
, associe le point 
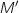d'affixe 
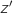définie par
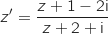
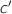du point C
, image de C par et placer le point C sur la figure.
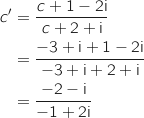On remarque que 
.
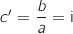des points d'affixe avec 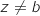, tels que 
.
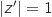On remarque que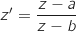 
donc, pour 
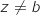on a :
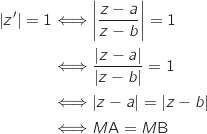Donc l'ensemble 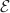est la médiatrice de [AB].
c. Justifier que 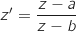donc, pour 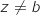on a :
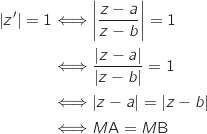Donc l'ensemble 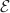est la médiatrice de [AB].
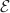contient les points O et C. Tracer .
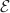- Comme OAB est isocèle en O, OAOB, donc O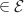
.
- On a vu que
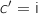donc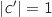 
, ce qui prouve que C
.
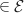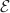, il suffit de tracer la droite (OC).
La dernière question de l'exercice original utilise des rotations qui ne sont plus au programme à partir de la
session 2013.
