Corrigé de l'exercice 2 du bac S de maths de novembre 2012 en Amérique du sud
Cacher les corrigés
Le plan complexe est muni d'un repère orthonormé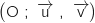 (unité graphique 2 cm).
On considère les points A, B et C d'affixes respectives
(unité graphique 2 cm).
On considère les points A, B et C d'affixes respectives
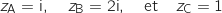
 qui à tout point
qui à tout point  du plan d'affixe
du plan d'affixe  , distinct de A, associe le point
, distinct de A, associe le point  d'affixe
d'affixe
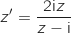
1. Déterminer l'ensemble des points
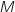 d'affixe
d'affixe  tels que
tels que 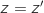 (ensemble des points invariants par la transformation
(ensemble des points invariants par la transformation  ).
).
Il s'agit de résoudre pour 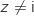 :
:
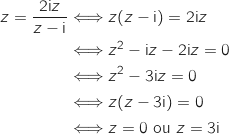 Donc la transformation admet 2 points invariants qui sont le point O et le point d'affixe
Donc la transformation admet 2 points invariants qui sont le point O et le point d'affixe 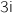 .
.
2. Déterminer, sous forme algébrique, les affixes des points B' et C', images respectives des points B et C par 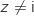 :
:
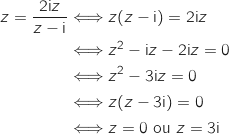 Donc la transformation admet 2 points invariants qui sont le point O et le point d'affixe
Donc la transformation admet 2 points invariants qui sont le point O et le point d'affixe 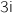 .
. .
.
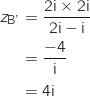
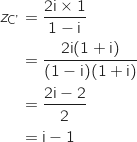
3.a. Montrer que, pour tout point
 distinct de A, l'affixe
distinct de A, l'affixe 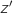 de
de 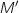 vérifie l'égalité :
vérifie l'égalité :
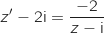
Pour 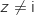 :
:
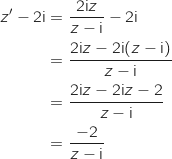
b. En déduire que si le point  :
:
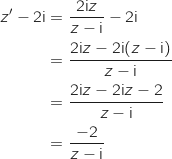
 appartient au cercle
appartient au cercle 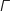 de centre A et de rayon 1,
alors son image
de centre A et de rayon 1,
alors son image 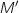 appartient à un cercle dont on déterminera le centre et le rayon.
appartient à un cercle dont on déterminera le centre et le rayon.
On interprète la relation précédente en terme de module :
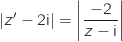 Si
Si  alors A
alors A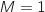 soit
soit 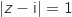 , donc l'égalité devient :
, donc l'égalité devient : 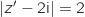 , ce qui traduit la relation B
, ce qui traduit la relation B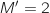 .
Donc le point M' appartient au cercle
.
Donc le point M' appartient au cercle 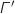 de centre B et de rayon 2.
de centre B et de rayon 2.
c. Exprimer une mesure de l'angle 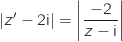 Si
Si  alors A
alors A soit
soit 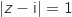 , donc l'égalité devient :
, donc l'égalité devient : 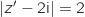 , ce qui traduit la relation B
, ce qui traduit la relation B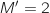 .
Donc le point M' appartient au cercle
.
Donc le point M' appartient au cercle 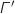 de centre B et de rayon 2.
de centre B et de rayon 2.
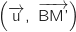 en fonction d'une mesure de l'angle
en fonction d'une mesure de l'angle 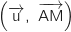 .
.
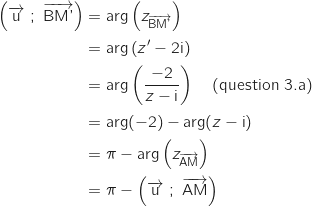
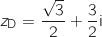 . Vérifier que D appartient au cercle
. Vérifier que D appartient au cercle 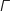 .
Construire, à la règle et au compas, le point D et son image D' par
.
Construire, à la règle et au compas, le point D et son image D' par  .
.
Pour vérifier que D appartient à  on calcule :
on calcule :
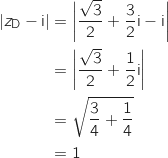 Donc D appartient bien à
Donc D appartient bien à  .
Pour construire D' à la règle et au compas on sait que :
.
Pour construire D' à la règle et au compas on sait que :
 sur le cercle
sur le cercle 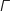 tel que
tel que 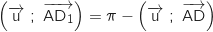 (D
(D est le symétrique de D par la symétrie d'axe
est le symétrique de D par la symétrie d'axe 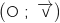 .
On construit la droite (AD
.
On construit la droite (AD ) et la droite parallèle à (AD
) et la droite parallèle à (AD ) qui passe par B, celle-ci coupe le cercle
) qui passe par B, celle-ci coupe le cercle  en deux points, le point D' est celui
pour lequel
en deux points, le point D' est celui
pour lequel 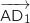 et
et 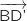 sont de même sens.
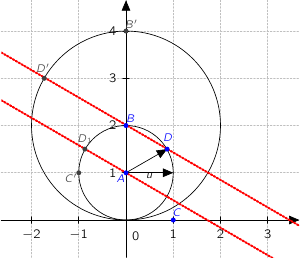
Figure :
sont de même sens.
Figure :
 on calcule :
on calcule :
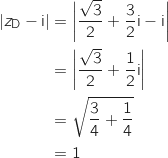 Donc D appartient bien à
Donc D appartient bien à 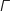 .
Pour construire D' à la règle et au compas on sait que :
.
Pour construire D' à la règle et au compas on sait que :
- D'
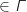 (question 3.b.)
(question 3.b.)
-
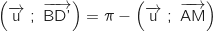
 sur le cercle
sur le cercle 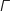 tel que
tel que 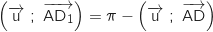 (D
(D est le symétrique de D par la symétrie d'axe
est le symétrique de D par la symétrie d'axe 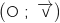 .
On construit la droite (AD
.
On construit la droite (AD ) et la droite parallèle à (AD
) et la droite parallèle à (AD ) qui passe par B, celle-ci coupe le cercle
) qui passe par B, celle-ci coupe le cercle 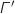 en deux points, le point D' est celui
pour lequel
en deux points, le point D' est celui
pour lequel 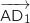 et
et 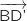 sont de même sens.
Figure :
sont de même sens.
Figure :

La dernière question du sujet original traite de barycentres. Les barycentres ne sont plus au programme depuis la rentrée 2012.
