Sujet et corrigé de l'exercice 4 du bac S de maths de mai 2013 en Amérique du nord
Cacher les corrigés
Soit la fonction définie sur l'intervalle
la fonction définie sur l'intervalle 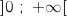 par
par
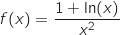
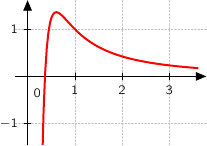
 la courbe représentative de la fonction
la courbe représentative de la fonction  dans un repère du plan. La courbe
dans un repère du plan. La courbe  est donnée ci-dessous :
est donnée ci-dessous :
1.a. Etudier la limite de
 en
en 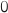 .
.
Limite à droite en 0
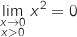 par valeurs positives ;
par valeurs positives ;
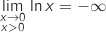 et en ajoutant 1 :
et en ajoutant 1 :
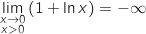 .
Enfin, par quotient
.
Enfin, par quotient 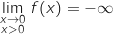 .
.
b. Que vaut 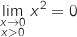 par valeurs positives ;
par valeurs positives ;
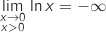 et en ajoutant 1 :
et en ajoutant 1 :
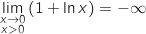 .
Enfin, par quotient
.
Enfin, par quotient 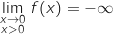 .
.
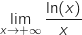 ? En déduire la limite de la fonction
? En déduire la limite de la fonction  en
en 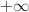 .
.
On sait que 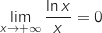 (par valeurs positives).
Pour déterminer la limite de
(par valeurs positives).
Pour déterminer la limite de  en
en  et lever l'indétermination en exploitant le résultat énoncé ci-dessus on écrit :
et lever l'indétermination en exploitant le résultat énoncé ci-dessus on écrit :
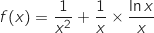 .
.
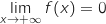 .
.
c. En déduire les asymptotes éventuelles à la courbe 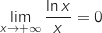 (par valeurs positives).
Pour déterminer la limite de
(par valeurs positives).
Pour déterminer la limite de  en
en  et lever l'indétermination en exploitant le résultat énoncé ci-dessus on écrit :
et lever l'indétermination en exploitant le résultat énoncé ci-dessus on écrit :
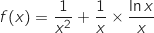 .
.
-
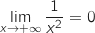
-
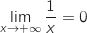 ;
;
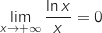 et par produit :
et par produit : 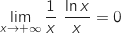 .
.
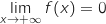 .
.
 .
.
Le résultat obtenu à la question a. entraîne que  admet une asymptote verticale d'équation
admet une asymptote verticale d'équation 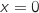 (axe des ordonnées).
Le résultat obtenu à la question b. entraîne que
(axe des ordonnées).
Le résultat obtenu à la question b. entraîne que  admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 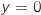 (axe des abscisses).
(axe des abscisses).
 admet une asymptote verticale d'équation
admet une asymptote verticale d'équation 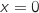 (axe des ordonnées).
Le résultat obtenu à la question b. entraîne que
(axe des ordonnées).
Le résultat obtenu à la question b. entraîne que  admet en
admet en  une asymptote horizontale d'équation
une asymptote horizontale d'équation 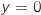 (axe des abscisses).
(axe des abscisses).
2.a. On note
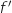 la fonction dérivée de la fonction
la fonction dérivée de la fonction  sur l'intervalle
sur l'intervalle 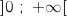 .
Démontrer que, pour tout réel
.
Démontrer que, pour tout réel  appartenant à l'intervalle
appartenant à l'intervalle 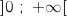 ,
,
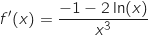
La fonction  est dérivable sur
est dérivable sur 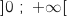 et on peut écrire :
et on peut écrire :
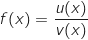 avec :
avec :
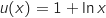 ;
; 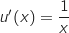
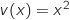 ;
; 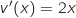
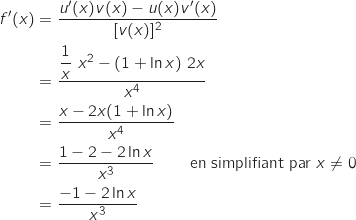
b. Résoudre sur l'intervalle  est dérivable sur
est dérivable sur 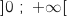 et on peut écrire :
et on peut écrire :
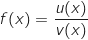 avec :
avec :
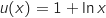 ;
; 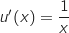
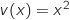 ;
; 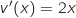
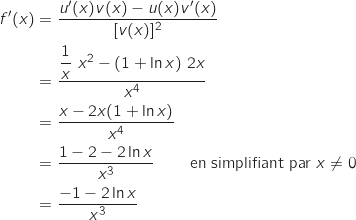
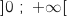 l'inéquation
l'inéquation 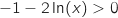 .
En déduire le signe de
.
En déduire le signe de 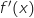 sur l'intervalle
sur l'intervalle 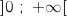 .
.
Sur 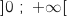 on a :
on a :
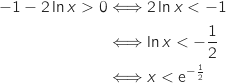 On a de même :
On a de même : 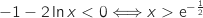 et
et
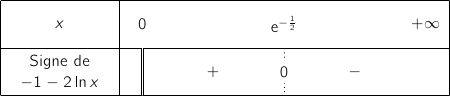
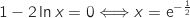 et on a le tableau de signes :
et on a le tableau de signes :
c. Dresser le tableau des variations de la fonction  on a :
on a :
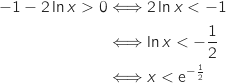 On a de même :
On a de même : 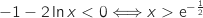 et
et
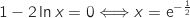 et on a le tableau de signes :
et on a le tableau de signes :

 .
.
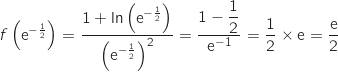 .
.
 a un unique point d'intersection avec l'axe des abscisses, dont on précisera les coordonnées.
a un unique point d'intersection avec l'axe des abscisses, dont on précisera les coordonnées.
On résout sur 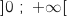 l'équation :
l'équation :
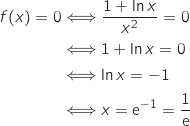 Du coup la fonction
Du coup la fonction  s'annule sur
s'annule sur 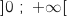 uniquement pour
uniquement pour 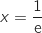 ce qui donne un unique point
d'intersection de
ce qui donne un unique point
d'intersection de  avec l'axe des abscisses dont les coordonnées sont
avec l'axe des abscisses dont les coordonnées sont 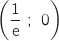 .
.
b. En déduire le signe de 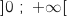 l'équation :
l'équation :
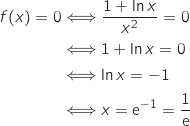 Du coup la fonction
Du coup la fonction  s'annule sur
s'annule sur 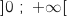 uniquement pour
uniquement pour 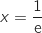 ce qui donne un unique point
d'intersection de
ce qui donne un unique point
d'intersection de  avec l'axe des abscisses dont les coordonnées sont
avec l'axe des abscisses dont les coordonnées sont 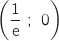 .
.
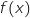 sur l'intervalle
sur l'intervalle 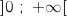 .
.
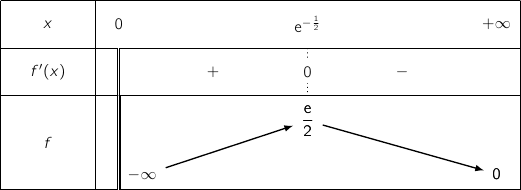
En exploitant ce qui précède on obtient facilement le tableau de signes :

4. Pour tout entier 
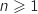 , on note
, on note 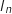 l'aire, exprimée en unités d'aires, du domaine délimité par l'axe des abscisses,
la courbe
l'aire, exprimée en unités d'aires, du domaine délimité par l'axe des abscisses,
la courbe  et les droites d'équations respectives
et les droites d'équations respectives 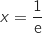 et
et 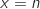 .
a. Démontrer que
.
a. Démontrer que 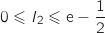 .
.
On peut déjà remarquer que pour tout 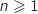 , la fonction
, la fonction  est continue et positive sur l'intervalle
est continue et positive sur l'intervalle 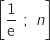 et du coup
et du coup
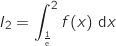 D'après l'étude des variations de la fonction
D'après l'étude des variations de la fonction  , pour tout
, pour tout 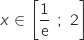 :
:
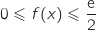 L'intégration de
L'intégration de  à 2 conserve l'ordre (car
à 2 conserve l'ordre (car 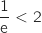 ) donc on a :
) donc on a :
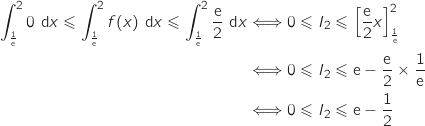
On admet que la fonction 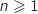 , la fonction
, la fonction  est continue et positive sur l'intervalle
est continue et positive sur l'intervalle 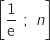 et du coup
et du coup
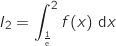 D'après l'étude des variations de la fonction
D'après l'étude des variations de la fonction  , pour tout
, pour tout 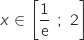 :
:
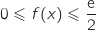 L'intégration de
L'intégration de  à 2 conserve l'ordre (car
à 2 conserve l'ordre (car 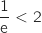 ) donc on a :
) donc on a :
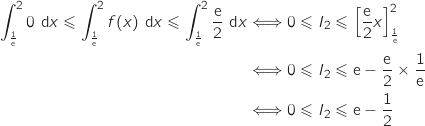
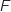 , définie sur l'intervalle
, définie sur l'intervalle 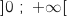 par
par 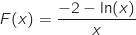 est une primitive de la fonction
est une primitive de la fonction  sur l'intervalle
sur l'intervalle 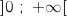 .
b. Calculer
.
b. Calculer 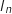 en fonction de
en fonction de  .
.
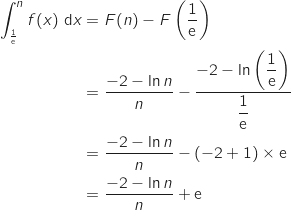
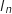 en
en 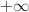 . Interpréter graphiquement le résultat obtenu.
. Interpréter graphiquement le résultat obtenu.
On écrit : 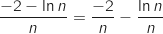 .
.
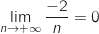 et
et
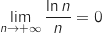 (limite connue) ;
donc
(limite connue) ;
donc 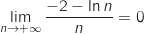 Finalement en ajoutant
Finalement en ajoutant  on obtient
on obtient 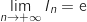 .
L'aire du domaine délimité par la droite d'équation
.
L'aire du domaine délimité par la droite d'équation 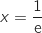 ; l'axe des abscisses et la courbe
; l'axe des abscisses et la courbe  vaut
vaut  u.a. (domaine illimité à droite).
u.a. (domaine illimité à droite).
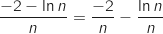 .
.
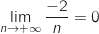 et
et
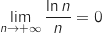 (limite connue) ;
donc
(limite connue) ;
donc 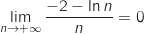 Finalement en ajoutant
Finalement en ajoutant  on obtient
on obtient 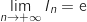 .
L'aire du domaine délimité par la droite d'équation
.
L'aire du domaine délimité par la droite d'équation 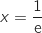 ; l'axe des abscisses et la courbe
; l'axe des abscisses et la courbe  vaut
vaut  u.a. (domaine illimité à droite).
u.a. (domaine illimité à droite).
