Corrigé de l'exercice 1 du bac S de maths de mai 2012 en Amérique du nord
Cacher les corrigés
Dans une association sportive, un quart des femmes et un tiers des hommes adhèrent à la section tennis. On sait également que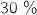 des membres de cette association adhèrent à la section tennis.
des membres de cette association adhèrent à la section tennis.
Partie A
On choisit au hasard un membre de cette association et on note :- F l'événement « le membre choisi est une femme »,
- T l'événement « le membre choisi adhère à la section tennis »,
1. Montrer que la probabilité de l'événement F est égale à
 .
.
On peut représenter la situation par un arbre de probabilité où 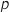 est la proportion inconnue de femmes dans l'association.
est la proportion inconnue de femmes dans l'association.
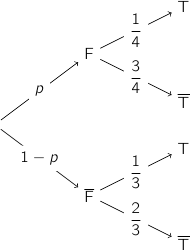
Les événements F et 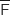 constituent un système complet d'événements, donc d'après la formule des probabilités totales on a :
constituent un système complet d'événements, donc d'après la formule des probabilités totales on a :
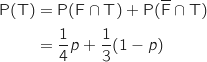 Comme on sait que
Comme on sait que 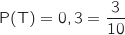 , on obtient l'équation :
, on obtient l'équation :
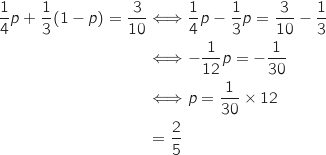 Donc
Donc 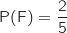 .
.
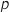 est la proportion inconnue de femmes dans l'association.
est la proportion inconnue de femmes dans l'association.

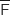 constituent un système complet d'événements, donc d'après la formule des probabilités totales on a :
constituent un système complet d'événements, donc d'après la formule des probabilités totales on a :
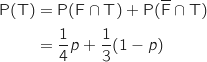 Comme on sait que
Comme on sait que 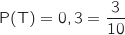 , on obtient l'équation :
, on obtient l'équation :
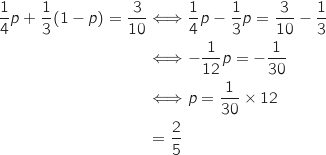 Donc
Donc 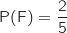 .
.
2. On choisit un membre parmi les adhérents à la section tennis. Quelle est la probabilité que ce membre soit une femme ?
En utilisant la formule de la probabilité conditionnelle on a :
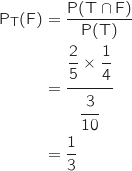
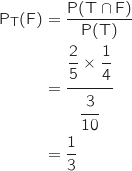
Partie B
Pour financer une sortie, les membres de cette association organisent une loterie. 1. Chaque semaine, un membre de l'association est choisi au hasard et de manière indépendante pour tenir la loterie. a. Déterminer la probabilité pour qu'en quatre semaines consécutives, il y ait exactement deux fois un membre qui adhère à la section tennis parmi les membres choisis.
On répète de manière indépendante 4 fois de suite une expérience de Bernoulli dont la probabilité du succès (obtenir un membre qui fait du tennis) est 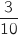 .
La variable aléatoire
.
La variable aléatoire 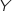 qui compte le nombre de fois qu'on a obtenu un joueur de tennis suit une loi binomiale
qui compte le nombre de fois qu'on a obtenu un joueur de tennis suit une loi binomiale 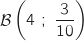 .
Donc
.
Donc 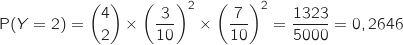 .
.
b. Pour tout entier naturel 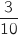 .
La variable aléatoire
.
La variable aléatoire 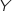 qui compte le nombre de fois qu'on a obtenu un joueur de tennis suit une loi binomiale
qui compte le nombre de fois qu'on a obtenu un joueur de tennis suit une loi binomiale 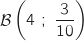 .
Donc
.
Donc 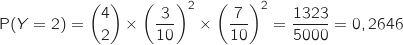 .
.
 non nul, on note
non nul, on note 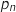 la probabilité pour qu'en
la probabilité pour qu'en  semaines consécutives, il y ait au moins un membre qui adhère à la section tennis parmi les membres
choisis.
Montrer que pour tout entier
semaines consécutives, il y ait au moins un membre qui adhère à la section tennis parmi les membres
choisis.
Montrer que pour tout entier  non nul,
non nul, 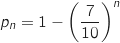 .
.
On est exactement dans la même situation que la question précédente sauf qu'on répète maintenant  fois l'expérience de Bernoulli (
fois l'expérience de Bernoulli ( entier naturel non nul), donc la variable aléatoire
entier naturel non nul), donc la variable aléatoire
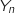 qui compte le nombre de fois où on a obtenu un joueur de tennis suit un loi binomiale
qui compte le nombre de fois où on a obtenu un joueur de tennis suit un loi binomiale 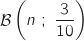 et on a :
et on a :
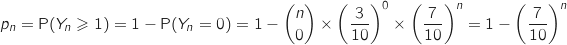 .
.
c. Déterminer le nombre minimal de semaines pour que  fois l'expérience de Bernoulli (
fois l'expérience de Bernoulli ( entier naturel non nul), donc la variable aléatoire
entier naturel non nul), donc la variable aléatoire
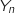 qui compte le nombre de fois où on a obtenu un joueur de tennis suit un loi binomiale
qui compte le nombre de fois où on a obtenu un joueur de tennis suit un loi binomiale 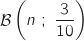 et on a :
et on a :
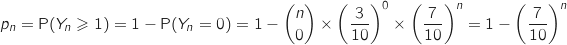 .
.
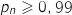 .
.
Il s'agit de résoudre :
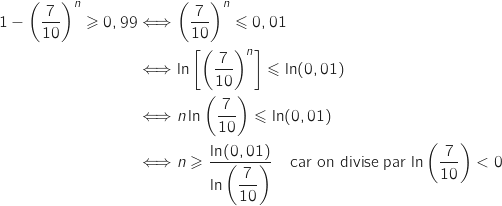 avec
avec 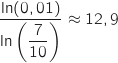 Donc il faut au minimum 13 semaines.
Donc il faut au minimum 13 semaines.
2. Pour cette loterie, on utilise une urne contenant 100 jetons ; 10 jetons exactement sont gagnants
et rapportent 20 euros chacun, les autres ne rapportent rien.
Pour jouer à cette loterie, un joueur doit payer 5 euros puis tire au hasard et de façon simultanée deux
jetons de l'urne : il reçoit alors 20 euros par jeton gagnant. Les deux jetons sont ensuite remis
dans l'urne.
On note 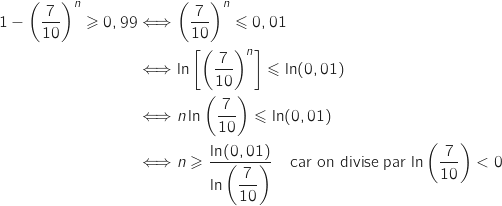 avec
avec 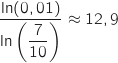 Donc il faut au minimum 13 semaines.
Donc il faut au minimum 13 semaines.
 la variable aléatoire associant le gain algébrique (déduction faite des 5 €) réalisé par un joueur lors d'une partie à cette loterie.
a. Déterminer la loi de probabilité de la variable aléatoire
la variable aléatoire associant le gain algébrique (déduction faite des 5 €) réalisé par un joueur lors d'une partie à cette loterie.
a. Déterminer la loi de probabilité de la variable aléatoire  .
.
Le tirage simultané de deux jetons est équivalent au tirage successif sans remise de 2 jetons.
On note :
J : « Le premier jeton est gagnant ».
J
: « Le premier jeton est gagnant ».
J : « Le deuxième jeton est gagnant ».
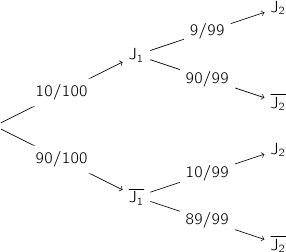
On peut représenter la situation par l'arbre de probabilités :
: « Le deuxième jeton est gagnant ».
On peut représenter la situation par l'arbre de probabilités :
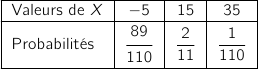
La variable aléatoire  peut prendre les valeurs :
peut prendre les valeurs :
 :
:
b. Calculer l'espérance mathématique de la variable aléatoire  : « Le premier jeton est gagnant ».
J
: « Le premier jeton est gagnant ».
J : « Le deuxième jeton est gagnant ».
On peut représenter la situation par l'arbre de probabilités :
: « Le deuxième jeton est gagnant ».
On peut représenter la situation par l'arbre de probabilités :

 peut prendre les valeurs :
peut prendre les valeurs :
- -5 : « le joueur a tiré deux jetons perdants »
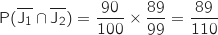
- 15 : « le joueur a tiré un jeton perdant et un jeton gagnant »
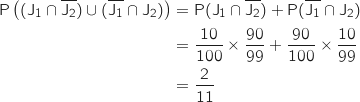
- 35 : « le joueur a tiré deux jetons gagnants »
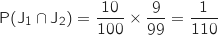
 :
:

 et interpréter le résultat obtenu.
et interpréter le résultat obtenu.
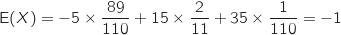 .
Le jeu est donc défavorable pour les joueurs.
Pour un grand nombre de parties, l'association peut espérer gagner 1 euro par partie.
.
Le jeu est donc défavorable pour les joueurs.
Pour un grand nombre de parties, l'association peut espérer gagner 1 euro par partie.
