Sujet et corrigé de l'exercice 3 du bac S de maths de juin 2016 en métropole
Cacher les corrigés
Partie A
Soit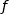 
la fonction définie sur 
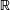par
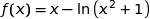
1. Résoudre dans 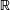l'équation : 
.
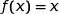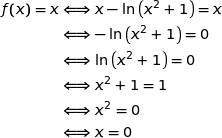
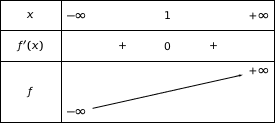
2. Justifier tous les éléments du tableau de variations ci-dessous à l'exception de la limite de la fonctio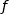n en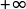 
que l'on admet.
La fonction 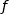est dérivable sur 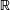et on a :
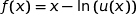
où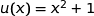 
; 
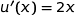
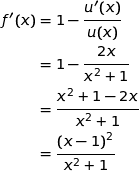
Pour tout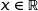 
, 
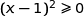et ne s'annule que pour 
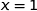et pour 
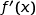c'est la même chose. Il s'ensuit que 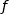est strictement croissante sur .
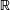Limite de 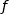en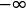 
:
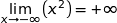et par somme 
.
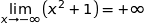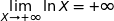; donc par composée :
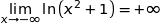
et en opposant :
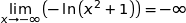
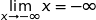et par somme :
.
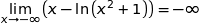3. Montrer que, pour tout réel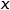 
appartenant à 
, 
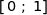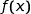appartient à .
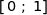Pour tout réel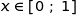 
:
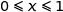
Comme par ailleurs 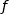est croissante sur 
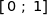, les images par 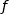sont rangées dans le même ordre soit :
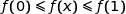
avec :
Du coup : 
.
4. On considère l'algorithme suivant :
a) Que fait cet algorithme ?
Cet algorithme détermine la plus petite valeur de 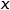entière telle que 
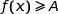où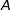 
est un nombre entier naturel entré par l'utilisateur.
b) Déterminer la valeur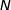 
fournie par l'algorithme lorsque la valeur saisie pour 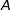est 100.
En utilisant la calculette on trouve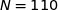 
.
Partie B
Soit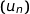 
la suite définie par 
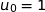et, pour tout entier naturel 
, 
.
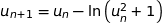1. Montrer par récurrence que, pour tout entier naturel , 
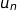appartient à .
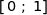Soit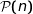 
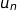: « appartient à ».
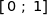Initialisation au rang 0
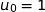, donc 
.
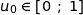Hérédité
Supposons que pour un entier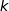 
, 
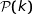soit vraie c'est à dire 
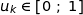; montrons qu'alors 
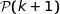est également vraie.
On remarque déjà que pour tout entier naturel , 
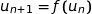où 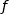est la fonction étudiée dans la partie A.
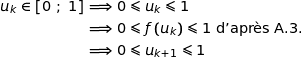
Donc 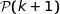est vraie.
Ainsi 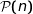est vraie pour 
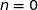et est héréditaire donc 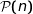est vraie pour tout entier naturel .
2. Etudier les variations de la suite .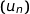
Pour tout entier naturel :
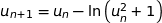
donc
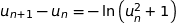
or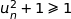 
donc 
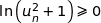et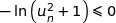 
.
Du coup pour tout entier naturel , 
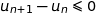soit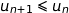 
ce qui montre que 
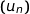est décroissante.
3. Montrer que la suite 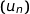est convergente.
Pour tout entier naturel , 
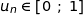, donc 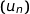est minorée par 0 et comme de plus la suite est décroissante on peut affirmer d'après le théorème de convergence monotone qu'elle converge.
4. On note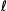 
sa limite, et on admet que 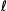vérifie l'égalité 
.
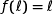En déduire la valeur de .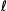
Il s'agit de résoudre l'équation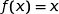 
.
En utilisant le résultat de A.1, on obtient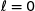 
.
