Sujet et corrigé de l'exercice 2 du bac S de maths de juin 2015 en métropole
Cacher les corrigés
Dans un repère orthonormé (O, I, J, K) d'unité 1 cm, on considère les points A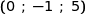
,
B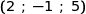
, C
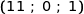, D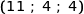
.
Un point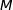 
se déplace sur la droite (AB) dans le sens de A vers B à la vitesse de 1 cm par seconde.
Un point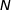 
se déplace sur la droite (CD) dans le sens de C vers D à la vitesse de 1 cm par seconde.
À l'instant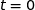 
le point 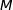est en A et le point 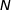est en C.
On note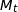 
et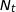 
les positions des points 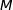et 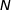au bout de 
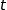secondes, 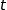désignant un nombre réel positif.
On admet que 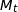et 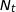, ont pour coordonnées :
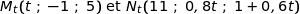
Les questions 1 et 2 sont indépendantes.
1.
a) La droite (AB) est parallèle à l'un des axes (OI), (OJ) ou (OK). Lequel ?
On calcule facilement les coordonnées du vecteur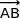 
:
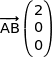
On remarque que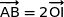 
, ce qui prouve que (AB) est parallèle à l'axe (OI).
b) La droite (CD) se trouve dans un plan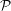 
parallèle à l'un des plans (OIJ), (OIK) ou (OJK).
Lequel ? On donnera une équation de ce plan .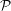
Les coordonnées du vecteur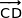 
sont :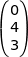 
On remarque que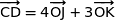 
.
Ainsi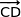 
est combinaison linéaire des deux vecteurs 
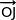et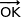 
, cela montre que la droite (CD) se trouve dans un plan parallèle au plan (OJK).
L'équation de ce plan est de la forme :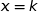 
.
C est dans le plan donc :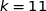 
.
Finalement l'équation de :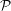 
.
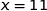c) Vérifier que la droite (AB), orthogonale au plan 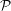, coupe ce plan au point 
.
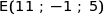E est déjà dans le plan 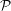car son abscisse vaut 11.
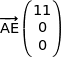est colinéaire à 
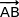car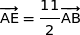 
, donc E est sur la droite (AB).
Ainsi E appartient à (AB) et à .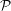
d) Les droites (AB) et (CD) sont-elles sécantes ?
On obtient facilement des représentations paramétriques des deux droites considérées :
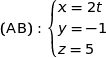
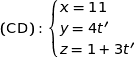
On résout le système avec ces deux représentations et on obtient :
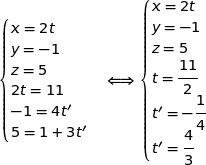
Donc le système n'a pas de solution : les droites ne sont pas sécantes.
2.
a) Montrer que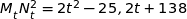 
.
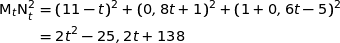
b) À quel instant 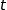la longueur 
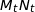est-elle minimale ?
Le minimum de la fonction trinôme du second degré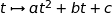 
est atteint pour 
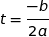, ce qui donne ici :
.
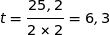