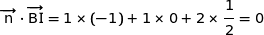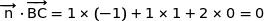Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2016 en Amérique du nord
Cacher les corrigés
On considère la pyramide régulière SABCD de sommet S constituée de la base carrée ABCD et de triangles équilatéraux représentée ci-dessous.
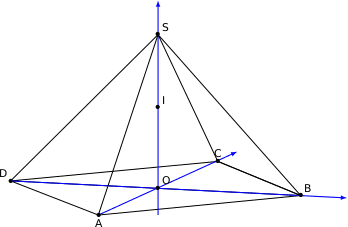
Le point O est le centre de la base ABCD avec OB 
.
On rappelle que le segment [SO] est la hauteur de la pyramide et que toutes les arêtes ont la même longueur.
1. Justifier que le repère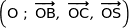 
est orthonormé.
Dans la suite de l'exercice, on se place dans le repère .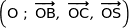
Les diagonales [AC] et [DB] du carré ABCD sont perpendiculaires et se coupent en leur milieu, il s'ensuit que les vecteurs 
et 
sont orthogonaux et que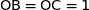 
.
Toutes les arêtes de la pyramide ont la même longueur donc le triangle SBD est isocèle en S et la médiane (SO) est perpendiculaire à (SD) ; par conséquent et 
sont orthogonaux.
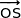En travaillant dans le triangle SCA, on montre de même que et sont orthogonaux.
Par conséquent les vecteurs 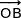, 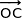et 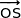sont deux à deux orthogonaux ce qui justifie que le repère est orthogonal.
Il nous reste à calculer OS pour le comparer à OB et OC.
On rappelle que pour un carré de côté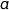 
la diagonale mesure 
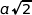et que dans un carré de diagonale 
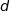, le côté mesure 
.
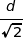Le carré ABCD a sa diagonale qui mesure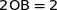 
et donc 
.
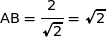Dans le triangle OSB rectangle en O on a d'après la propriété de Pythagore :
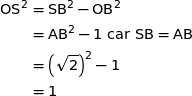
Donc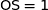 
et cela termine de montrer que le repère considéré est orthonormé.
2. On définit le point K par la relation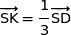 
et on note I le milieu du segment [SO].
a) Déterminer les coordonnées du point K.
Dans le repère :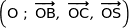
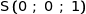
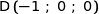
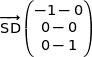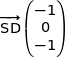
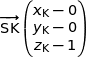soit 
soit 
La relation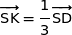 
donne :
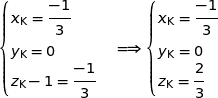
Donc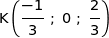 
.
b) En déduire que les points B, I et K sont alignés.
Dans le repère :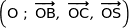
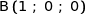
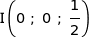
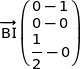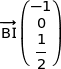
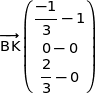soit 
soit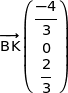 
Donc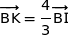 
ce qui prouve que 
et 
sont colinéaires et que B, K et I sont alignés.
c) On note L le point d'intersection de l'arête [SA] avec le plan (BCI).
Justifier que les droites (AD) et (KL) sont parallèles.
D'après la question précédente B, K et I sont alignés donc K appartient au plan (BCI) puisque ce point se trouve sur la droite (BI) incluse dans le plan.
Le point L appartient également au plan (BCI) par définition.
Ainsi K et L sont deux points distincts de (BCI).
Le point K appartient à (SD) donc K appartient au plan (SAD).
Le point L appartient à (SA) par définition donc L appartient également à (SAD).
Du coup K et L sont deux points distincts qui appartiennent tous les deux aux deux plans non parallèles (SAD) et (BCI), donc (KL) est la droite d'intersection de ces deux plans.
On remarque de plus que les deux plans considérés contiennent respectivement les droites (AD) et (CB) qui sont parallèles et donc d'après le théorème du toit la droite d'intersection (KL) est parallèle à (AD) (et aussi à (BC)).
d) Déterminer les coordonnées du point L.
Dans le triangle SAD nous sommes en présence d'une configuration de Thalès avec la droite (KL) parallèle à (AD), par conséquent l'égalité 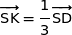entraîne l'égalité 
.
-
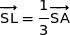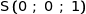
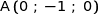
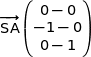soit 
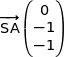
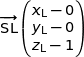soit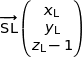 
L'égalité 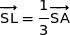donne :
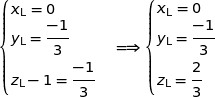
Soit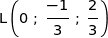 
.
3. On considère le vecteur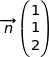 
dans le repère .
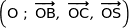a) Montrer que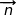 
est un vecteur normal au plan (BCI).
On a déjà vu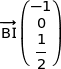
-
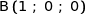
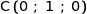
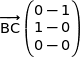soit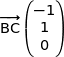 
Dans le repère orthonormé :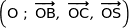
Cela prouve que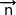 
est orthogonal à deux vecteurs non colinéaires du plan (BCI) donc 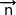est normal à ce plan.
b) Montrer que les vecteurs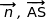 
et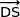 
sont coplanaires.
-
-
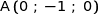
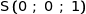
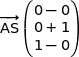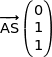
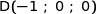
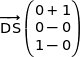soit 
soit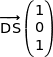 
Observons les 3 vecteurs :
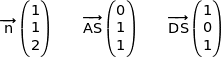
On remarque très facilement que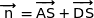 
Cette relation montre que ;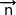 
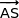et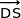 
sont coplanaires.
c) Quelle est la position relative des plans (BCI) et (SAD) ?
On sait déjà que (BCI) et (SAD) sont sécants selon la droite (KL). Par ailleurs le vecteur 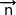normal à (BCI) est dans le plan (SAD) d'après la question précédente ; donc (BCI) et (SAD) sont perpendiculaires.
