Corrigé de l'exercice 4 du bac ES de maths d'avril 2013 à Pondichéry
Cacher les corrigés
PARTIE A
On désigne par la fonction définie sur l'intervalle
la fonction définie sur l'intervalle 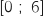 par
par
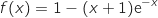
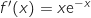 où
où 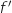 désigne la fonction dérivée de la fonction
désigne la fonction dérivée de la fonction  .
.
On peut écrire 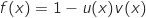 avec :
avec : 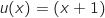 et
et 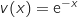 d'où :
d'où : 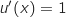 et
et 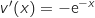
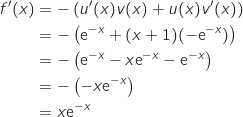
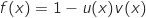 avec :
avec : 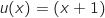 et
et 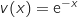 d'où :
d'où : 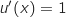 et
et 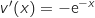
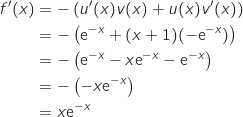
2. Démontrer que l'équation
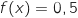 admet une solution unique
admet une solution unique 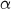 sur l'intervalle
sur l'intervalle 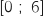 .
Déterminer une valeur arrondie de
.
Déterminer une valeur arrondie de 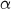 à 0,01.
à 0,01.
Sur 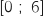 ,
, 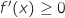 et
et 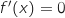 uniquement pour
uniquement pour 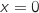 , donc
, donc  est strictement croissante sur l'intervalle considéré et on
a le tableau de variations :
est strictement croissante sur l'intervalle considéré et on
a le tableau de variations :
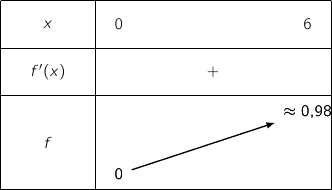
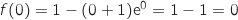
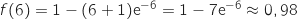 La fonction
La fonction  est continue et strictement croissante sur
est continue et strictement croissante sur 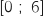 avec
avec 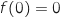 et
et 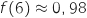 .
Donc on a
.
Donc on a 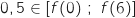 et du coup d'après le théorème des valeurs intermédiaires l'équation
et du coup d'après le théorème des valeurs intermédiaires l'équation 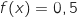 admet une unique solution
admet une unique solution 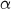 sur
sur 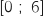 .
En utilisant la calculette on trouve
.
En utilisant la calculette on trouve 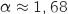 .
.
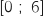 ,
, 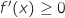 et
et 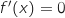 uniquement pour
uniquement pour 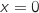 , donc
, donc  est strictement croissante sur l'intervalle considéré et on
a le tableau de variations :
est strictement croissante sur l'intervalle considéré et on
a le tableau de variations :

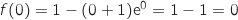
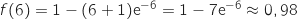 La fonction
La fonction  est continue et strictement croissante sur
est continue et strictement croissante sur 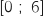 avec
avec 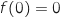 et
et 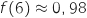 .
Donc on a
.
Donc on a 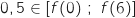 et du coup d'après le théorème des valeurs intermédiaires l'équation
et du coup d'après le théorème des valeurs intermédiaires l'équation 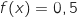 admet une unique solution
admet une unique solution 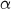 sur
sur 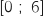 .
En utilisant la calculette on trouve
.
En utilisant la calculette on trouve 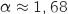 .
.
3. On admet que la fonction F définie sur
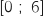 par :
par :
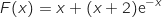
 sur
sur 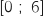 .
Donner la valeur exacte puis une valeur arrondie à
.
Donner la valeur exacte puis une valeur arrondie à  de
de 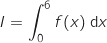 .
.
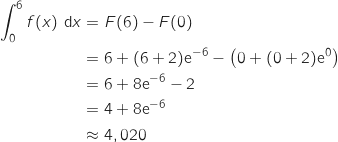
PARTIE B
Une entreprise lance la production de batteries pour véhicules électriques. Une étude a modélisé le rythme de la production journalière sur les six premiers mois à l'aide de la fonction définie dans la partie A pour
définie dans la partie A pour  compris entre 0 et 6.
compris entre 0 et 6.
 représente le nombre de mois (de 30 jours) depuis le lancement du produit.
représente le nombre de mois (de 30 jours) depuis le lancement du produit.
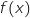 représente la production journalière de batteries en milliers.
1. Exprimer en mois puis en jours le moment où la production atteindra 0,5 millier soit 500 unités.
représente la production journalière de batteries en milliers.
1. Exprimer en mois puis en jours le moment où la production atteindra 0,5 millier soit 500 unités.
Il s'agit de résoudre l'équation 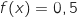 .
On sait d'après la question A.2. que l'unique solution sur
.
On sait d'après la question A.2. que l'unique solution sur 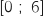 de cette équation est environ 1,68.
Donc la production atteindra 500 unités au bout de 1,68 mois soit environ 50 jours (
de cette équation est environ 1,68.
Donc la production atteindra 500 unités au bout de 1,68 mois soit environ 50 jours (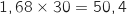 ).
).
2. Déterminer une valeur arrondie à 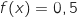 .
On sait d'après la question A.2. que l'unique solution sur
.
On sait d'après la question A.2. que l'unique solution sur 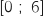 de cette équation est environ 1,68.
Donc la production atteindra 500 unités au bout de 1,68 mois soit environ 50 jours (
de cette équation est environ 1,68.
Donc la production atteindra 500 unités au bout de 1,68 mois soit environ 50 jours (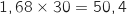 ).
).
 de la valeur moyenne, exprimée en milliers, de la production sur les six premiers mois.
de la valeur moyenne, exprimée en milliers, de la production sur les six premiers mois.
Il s'agit de déterminer la valeur moyenne de  sur
sur 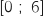 :
:
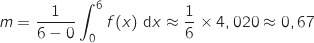 .
Donc la production moyenne sur les 6 premiers mois est d'environ 0,67 milliers de batteries.
.
Donc la production moyenne sur les 6 premiers mois est d'environ 0,67 milliers de batteries.
 sur
sur 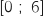 :
:
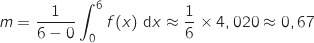 .
Donc la production moyenne sur les 6 premiers mois est d'environ 0,67 milliers de batteries.
.
Donc la production moyenne sur les 6 premiers mois est d'environ 0,67 milliers de batteries.
PARTIE C
Il est prévu que l'autonomie permise par ce type de batteries, sous certaines conditions de conduite, soit de 200 km. Sur un parcours joignant une ville située à 160 km, on suppose que l'autonomie, exprimée en km, permise par ces batteries suit une loi normale d'espérance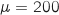 et d'écart-type
et d'écart-type 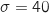 .
1. Quelle est la probabilité, arrondie au centième, de ne pas atteindre cette ville ?
.
1. Quelle est la probabilité, arrondie au centième, de ne pas atteindre cette ville ?
Soit  la variable aléatoire qui donne l'autonomie des battteries.
Il s'agit de calculer
la variable aléatoire qui donne l'autonomie des battteries.
Il s'agit de calculer 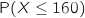 , où
, où  suit la loi normale indiquée dans l'énoncé.
En utilisant la calculette on obtient directement :
suit la loi normale indiquée dans l'énoncé.
En utilisant la calculette on obtient directement : 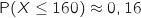 .
Donc la probabilité de ne pas atteindre la ville est d'environ 0,16.
.
Donc la probabilité de ne pas atteindre la ville est d'environ 0,16.
2. La probabilité de pouvoir faire l'aller-retour jusqu'à cette ville sans recharge des batteries est-elle supérieure à 0,01 ? Justifier votre réponse.
 la variable aléatoire qui donne l'autonomie des battteries.
Il s'agit de calculer
la variable aléatoire qui donne l'autonomie des battteries.
Il s'agit de calculer 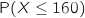 , où
, où  suit la loi normale indiquée dans l'énoncé.
En utilisant la calculette on obtient directement :
suit la loi normale indiquée dans l'énoncé.
En utilisant la calculette on obtient directement : 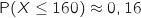 .
Donc la probabilité de ne pas atteindre la ville est d'environ 0,16.
.
Donc la probabilité de ne pas atteindre la ville est d'environ 0,16.
L'aller-retour représente 320 km, en utilisant la calculette on a :
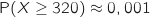 .
Donc la probabilité de pouvoir faire l'aller-retour est inférieure à 0,01.
.
Donc la probabilité de pouvoir faire l'aller-retour est inférieure à 0,01.
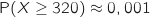 .
Donc la probabilité de pouvoir faire l'aller-retour est inférieure à 0,01.
.
Donc la probabilité de pouvoir faire l'aller-retour est inférieure à 0,01.
