Corrigé de l'exercice 1 du bac ES de maths d'avril 2013 à Pondichéry
Cacher les corrigés
Cet exercice est un questionnaire à choix multiples. Une réponse exacte rapporte 1 point. Une réponse fausse ou l'absence de réponse ne rapporte ni n'enlève aucun point. Pour chacune des questions posées, une seule des quatre réponses est exacte. Indiquer sur la copie le numéro de la question et recopier la réponse choisie. Aucune justification n'est demandée.
1. La fonction
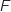 définie sur
définie sur 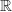 par
par 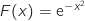 est une primitive de la fonction
est une primitive de la fonction  définie par :
A :
définie par :
A : 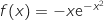 B :
B : 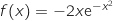 C :
C : 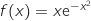 D :
D : 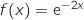
Pour trouver la bonne réponse il faut dériver 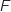 :
:
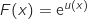 avec
avec 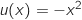 et donc
et donc 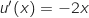 En utilisant la formule de dérivation :
En utilisant la formule de dérivation : 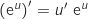 on obtient :
on obtient :
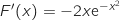 La bonne réponse est B.
La bonne réponse est B.
2. Soit la fonction 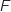 :
:
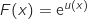 avec
avec 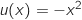 et donc
et donc 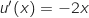 En utilisant la formule de dérivation :
En utilisant la formule de dérivation : 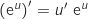 on obtient :
on obtient :
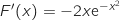 La bonne réponse est B.
La bonne réponse est B.
 définie sur
définie sur 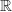 par
par 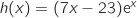 .
L'équation
.
L'équation 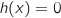 A : a pour solution 2,718
B : a une solution sur
A : a pour solution 2,718
B : a une solution sur 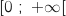 C : a deux solutions sur
C : a deux solutions sur 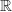 D : a une solution sur
D : a une solution sur 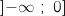
Pour tout 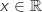 ,
, 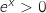 , donc ne s'annule pas.
L'équation est équivalente à
, donc ne s'annule pas.
L'équation est équivalente à 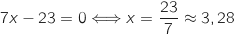 .
La bonne réponse est B
.
La bonne réponse est B
 ,
, 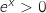 , donc ne s'annule pas.
L'équation est équivalente à
, donc ne s'annule pas.
L'équation est équivalente à 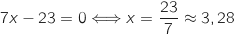 .
La bonne réponse est B
.
La bonne réponse est B
3. On pose
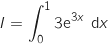 .
On peut affirmer que :
A :
.
On peut affirmer que :
A : 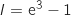 B :
B : 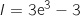 C :
C : 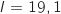 D :
D : 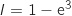
Une primitive de la fonction 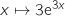 est la fonction
est la fonction 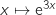 donc :
donc :
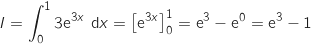 La bonne réponse est A.
La bonne réponse est A.
4. La fonction 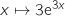 est la fonction
est la fonction 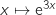 donc :
donc :
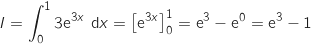 La bonne réponse est A.
La bonne réponse est A.
 définie sur
définie sur 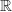 par
par 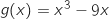 est convexe sur l'intervalle :
A :
est convexe sur l'intervalle :
A : 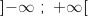 B :
B : 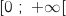 C :
C : 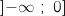 D :
D : 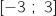 .
.
La dérivée de  est telle que
est telle que 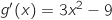 et la dérivée seconde est telle que
et la dérivée seconde est telle que 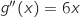 .
.
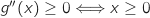 , donc
, donc  est convexe sur
est convexe sur 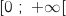 .
La bonne réponse est B.
.
La bonne réponse est B.
 est telle que
est telle que 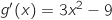 et la dérivée seconde est telle que
et la dérivée seconde est telle que 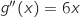 .
.
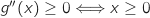 , donc
, donc  est convexe sur
est convexe sur 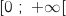 .
La bonne réponse est B.
.
La bonne réponse est B.
