Sujet et corrigé de l'exercice 4 du bac ES de maths de juin 2013 dans les centres étrangers
Cacher les corrigés
Tous les jours, Guy joue à un jeu en ligne sur un site, avec trois amis.
1. Paul se connecte sur le site. La durée
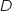 (en seconde) qu'il faut pour réunir les quatre joueurs est une variable aléatoire qui suit une loi uniforme sur l'intervalle
(en seconde) qu'il faut pour réunir les quatre joueurs est une variable aléatoire qui suit une loi uniforme sur l'intervalle 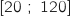 .
a. Déterminer la probabilité que les quatre joueurs soient réunis au bout de 60 secondes.
.
a. Déterminer la probabilité que les quatre joueurs soient réunis au bout de 60 secondes.
Sachant que 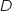 suit une loi uniforme sur
suit une loi uniforme sur 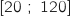 on a :
on a :
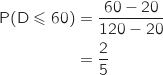
b. Calculer l'espérance mathématique de  suit une loi uniforme sur
suit une loi uniforme sur 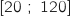 on a :
on a :
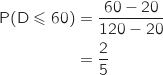
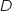 . Interpréter ce résultat.
. Interpréter ce résultat.
Comme 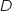 suit une loi uniforme sur
suit une loi uniforme sur 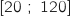 on a :
E
on a :
E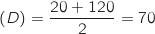 Cela signifie qu'en moyenne les quatre joueurs sont réunis au bout de 70 secondes.
Cela signifie qu'en moyenne les quatre joueurs sont réunis au bout de 70 secondes.
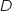 suit une loi uniforme sur
suit une loi uniforme sur 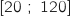 on a :
E
on a :
E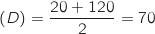 Cela signifie qu'en moyenne les quatre joueurs sont réunis au bout de 70 secondes.
Cela signifie qu'en moyenne les quatre joueurs sont réunis au bout de 70 secondes.
2. L'équipe est maintenant réunie et la partie peut commencer. La durée
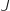 (en minute) d'une partie est une variable aléatoire qui suit la loi normale
(en minute) d'une partie est une variable aléatoire qui suit la loi normale 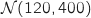 .
a. Déterminer l'espérance et l'écart-type de la variable aléatoire
.
a. Déterminer l'espérance et l'écart-type de la variable aléatoire 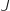 .
.
Comme 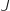 suit une loi
suit une loi 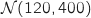 , l'espérance de
, l'espérance de 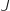 est 120 et sa variance
est 400. Donc l'écart-type de
est 120 et sa variance
est 400. Donc l'écart-type de 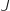 vaut
vaut 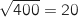 .
.
b. Montrer l'équivalence :
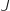 suit une loi
suit une loi 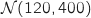 , l'espérance de
, l'espérance de 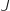 est 120 et sa variance
est 400. Donc l'écart-type de
est 120 et sa variance
est 400. Donc l'écart-type de 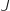 vaut
vaut 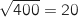 .
.
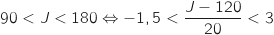
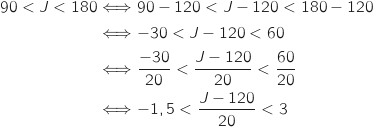
 par
par 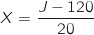 .
Déterminer la loi suivie par la variable aléatoire
.
Déterminer la loi suivie par la variable aléatoire  .
.
La variable aléatoire  est la variable aléatoire centrée et réduite associée à
est la variable aléatoire centrée et réduite associée à  .
Comme
.
Comme 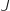 suit une loi normale,
suit une loi normale,  suit la loi normale standard
suit la loi normale standard 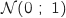 , c'est
à dire de moyenne 0 et d'écart-type 1.
, c'est
à dire de moyenne 0 et d'écart-type 1.
d. Déterminer la probabilité que la partie dure entre 90 et 180 minutes, à 0,001 près.
 est la variable aléatoire centrée et réduite associée à
est la variable aléatoire centrée et réduite associée à 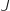 .
Comme
.
Comme 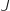 suit une loi normale,
suit une loi normale,  suit la loi normale standard
suit la loi normale standard 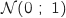 , c'est
à dire de moyenne 0 et d'écart-type 1.
, c'est
à dire de moyenne 0 et d'écart-type 1.
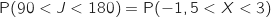 d'après la question b.
Avec la calculette on peut au choix calculer
d'après la question b.
Avec la calculette on peut au choix calculer 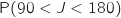 (loi
(loi 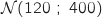 )
ou
)
ou 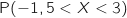 (loi normale standard).
Dans les deux cas on trouve environ 0,932.
(loi normale standard).
Dans les deux cas on trouve environ 0,932.
