Sujet et corrigé de l'exercice 4 du bac S de maths de juin 2015 en Amérique du nord

Cacher les corrigés

Soit la fonction définie sur par :

1. Justifier que la fonction est strictement croissante sur l'intervalle .

La fonction est strictement croissante sur .

Donc la fonction est également strictement croissante sur l'intervalle considéré comme somme de deux fonctions strictement croissantes.

2. Démontrer que l'équation admet une unique solution comprise entre 2 et 3.

La fonction est continue et strictement croissante sur avec :

Comme , d'après le théorème de la valeur intermédiaire l'équation admet une unique solution dans .

De plus :

Du coup et donc .

3. En déduire le signe de en fonction de .

Soit la fonction définie sur l'intervalle par :

On appelle la courbe représentative de la fonction dans un repère orthogonal.

1. Déterminer la limite de la fonction en 0.

Par produit : .

Finalement en ajoutant 2 : .

2.a. Démontrer que, pour tout réel de l'intervalle :

où est la fonction définie dans la partie A.

La fonction est dérivable sur et on a :

avec :

b. En déduire le sens de variation de la fonction sur l'intervalle .

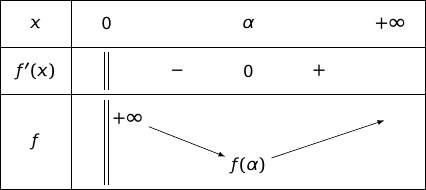
Pour tout ; donc le signe de est le même que celui de et du coup on a le tableau de variations :

Soit la courbe d'équation .

1. Démontrer que, pour tout réel de l'intervalle ,

En déduire que les courbes et ont un seul point commun dont on déterminera les coordonnées.

Pour tout réel on a :

Les abscisses des points communs éventuels de et sont les solutions sur de l'équation :

Donc et se coupent au point d'abscisse .

Le point d'intersection a pour coordonnées soit .

2. On admet que la fonction définie sur l'intervalle par est une primitive de la fonction définie sur l'intervalle par .

Calculer .

Interpréter graphiquement ce résultat.

On peut écrire

Pour , le signe de est le même que celui de :

Du coup, pour tout , et l'intégrale représente l'aire en u.a. du domaine délimité par les droites d'équations ; et les courbes et .